
【题目】为了方便广大游客到昆明参观游览,铁道部门临时增开了一列南宁——昆明的直达快车,已知南宁、昆明两站的路程为828千米,一列普通快车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普通快车平均速度的1.5倍,直达快车比普通快车后出发2小时,而先于普通快车4小时到达昆明,分别求出两车的速度.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
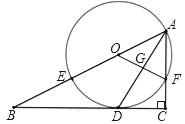
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点.
(1)如图①,若点E在![]() 上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;
上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;
(2)在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:DE﹣BE=![]() AE.请你说明理由;
AE.请你说明理由;
(3)如图②,若点E在![]() 上.写出线段DE、BE、AE之间的等量关系.(不必证明)
上.写出线段DE、BE、AE之间的等量关系.(不必证明)
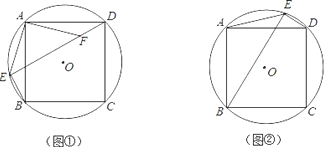
第26题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
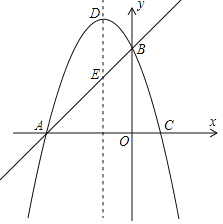
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系xOy中,一次函数y1=k1x+b(k≠0)的图象与反比例函数![]() (x>0)的图象交于A(1,4),B(3,m)两点.
(x>0)的图象交于A(1,4),B(3,m)两点.
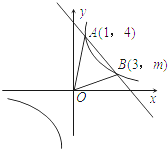
(1)试确定上述反比例函数和一次函数的表达式;
(2)在第一象限内,x取何值时,一次函数的函数值大于反比例函数的函数值;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
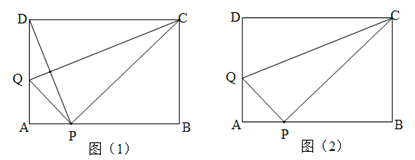
【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
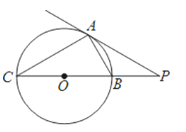
【题目】如图,点P是⊙O外一点,过点P作⊙O的切线,切点为A,连接PO并延长,交⊙O于B、C两点.
(1)求证:△PBA∽△PAC;
(2)若∠BAP=30°,PB=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
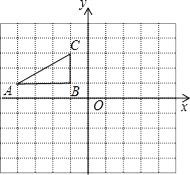
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程以及Rt△A1B1C1扫过的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
人数(人) | 8 | 12 | 10 | 6 | 2 | 2 |
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com