
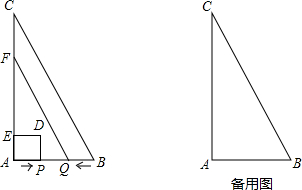
分析 (1)当点P与点Q重合时,此时AP=BQ=t,且AP+BQ=AB=2,由此列一元一次方程求出t的值;
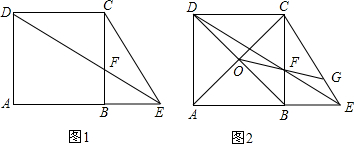
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.由相似三角形比例线段关系可得PQ=$\frac{1}{2}$t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段:
①当1<t≤$\frac{4}{3}$时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
②当$\frac{4}{3}$<t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE-S△AQF-S△DMN”求出.
解答 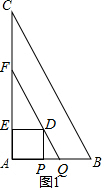 解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
∴t+t=2,解得t=1s,
故答案:1.
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.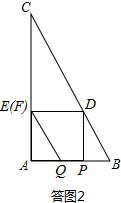
∵QF∥BC,APDE为正方形,
∴△PQD∽△ABC,
∴DP:PQ=AC:AB=2,
则PQ=$\frac{1}{2}$DP=$\frac{1}{2}$AP=$\frac{1}{2}$t.
由AP+PQ+BQ=AB=2,得t+$\frac{1}{2}$t+t=2,
解得:t=$\frac{4}{5}$.
故答案:$\frac{4}{5}$.
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=$\frac{1}{2}$t,
求得t=$\frac{4}{3}$s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤$\frac{4}{3}$时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,
∴AQ=2-t,PQ=AP-AQ=2t-2;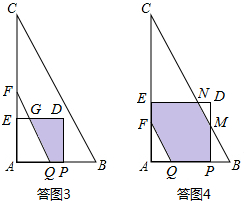
易知△ABC∽△AQF,
可得AF=2AQ,EF=2EG.
∴EF=AF-AE=2(2-t)-t=4-3t,EG=$\frac{1}{2}$EF=2-$\frac{3}{2}$t,
∴DG=DE-EG=t-(2-$\frac{3}{2}$t)=$\frac{5}{2}$t-2.
S=S梯形PDGQ=$\frac{1}{2}$(PQ+DG)•PD,
=$\frac{1}{2}$[(2t-2)+($\frac{5}{2}$t-2)]•t,
=$\frac{9}{4}$t2-2t;
②当$\frac{4}{3}$<t<2时,如答图4所示,此时重合部分为一个多边形.
此时AP=BQ=t,
∴AQ=PB=2-t,
易知△ABC∽△AQF∽△PBM∽△DNM,
可得AF=2AQ,PM=2PB,DM=2DN,
∴AF=4-2t,PM=4-2t.
又∵DM=DP-PM=t-(4-2t)=3t-4,
∴DN=$\frac{1}{2}$(3t-4)=$\frac{3}{2}$t-2,DM=3t-4.
S=S正方形APDE-S△AQF-S△DMN=AP2-$\frac{1}{2}$AQ•AF-$\frac{1}{2}$DN•DM
=t2-$\frac{1}{2}$(2-t)(4-2t)-$\frac{1}{2}$×$\frac{1}{2}$(3t-4)×(3t-4)
=-$\frac{9}{4}$t2+10t-8.
综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{\frac{9}{4}{t}^{2}-2t(1<t≤\frac{4}{3})}\\{-\frac{9}{4}{t}^{2}+10t-8(\frac{4}{3}<t<2)}\end{array}\right.$.
点评 此题主要考查了相似形综合题,函数解析式的求法,分析推理能力、空间想象能力的应用,分类讨论思想的应用,行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
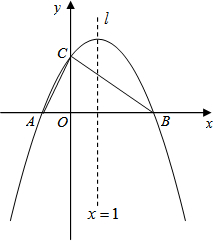 如图,在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
如图,在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com