
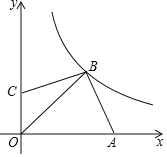
【题目】如图所示平面直角坐标系中,点A,C分别在x轴和y轴上,点B在第一象限,BC=BA,∠ABC=90°,反比例函数y=![]() .(x>0)的图象经过点B,若OB=2
.(x>0)的图象经过点B,若OB=2![]() ,则k的值为_____.
,则k的值为_____.
科目:初中数学 来源: 题型:
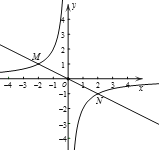
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象分别交于M,N两点,已知点M(-2,m).
的图象分别交于M,N两点,已知点M(-2,m).
(1)求反比例函数的表达式;
(2)点P为y轴上的一点,当∠MPN为直角时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,以BC为底边向正方形外部作等腰直角三角形BCE,连接AE,分别交BD,BC于点F,G,则下列结论:①△AFB∽△ABE;②△ADF∽△GCE;③CG=3BG;④AF=EF,其中正确的有( ).
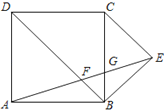
A.①③B.②④C.①②D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
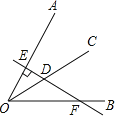
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
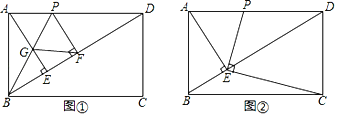
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AEAB=DEAP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
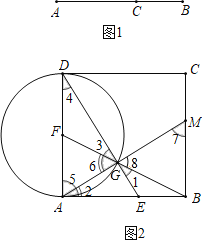
【题目】阅读下列材料,完成相应的学习任务:如图(1)在线段AB上找一点C,C把AB分为AC和BC两条线段,其中AC>BC.若AC,BC,AB满足关系AC2=BCAB.则点C叫做线段AB的黄金分割点,这时![]() =
=![]() ≈0.618,人们把
≈0.618,人们把![]() 叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
第一步,以AB为边作正方形ABCD.
第二步,以AD为直径作⊙F.
第三步,连接BF与⊙F交于点G.
第四步,连接DG并延长与AB交于点E,则E就是线段AB的黄金分割点.
证明:连接AG并延长,与BC交于点M.
∵AD为⊙F的直径,
∴∠AGD=90°,
∵F为AD的中点,
∴DF=FG=AF,
∴∠3=∠4,∠5=∠6,
∵∠2+∠5=90°,∠5+∠4=90°,
∴∠2=∠4=∠3=∠1,
∵∠EBG=∠GBA,
∴△EBG∽△GBA,
∴![]() =
=![]() ,
,
∴BG2=BEAB…
任务:
(1)请根据上面操作步骤与部分证明过程,将剩余的证明过程补充完整;(提示:证明BM=BG=AE)
(2)优选法是一种具有广泛应用价值的数学方法,优选法中有一种0.618法应用了黄金分割数.为优选法的普及作出重要贡献的我国数学家是 (填出下列选项的字母代号)
A.华罗庚
B.陈景润
C.苏步青
查看答案和解析>>
科目:初中数学 来源: 题型:
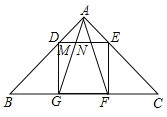
【题目】如图,在△ABC中,AB=AC=3![]() ,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于点M和点N,则线段MN的长为_____.
,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于点M和点N,则线段MN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).

(1)如图1,若![]() 平分
平分![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .①求证:
.①求证:![]() ;②若
;②若![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() .求证:
.求证:![]() 为
为![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
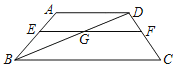
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com