
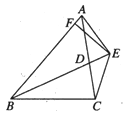
【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.
【答案】①②③⑤
【解析】①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,
∴在△ABD和△EBC中, 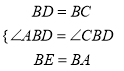 ,
,
∴△ABD≌△EBC(SAS),故①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,故②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,故③正确;
⑤过E作EG⊥BC于G点,

∵E是BD上的点,∴EF=EG,
∵在RT△BEG和RT△BEF中, ![]() ,
,
∴RT△BEG≌RT△BEF(HL),
∴BG=BF,
∵在RT△CEG和RT△AFE中, ![]() ,
,
∴RT△CEG≌RT△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BGCG=BF+BG=2BF,故⑤正确;
无法证明④正确.
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
【题目】如图是某同学在课下设计的一款软件,蓝精灵从点O第一跳落到A1(1,0),第二跳落到A2(1,2),第三跳落到A3(4,2),第四跳落到A4(4,6),第五跳落到A5________,到达A2n后,要向________方向跳________个单位长度落到A2n+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点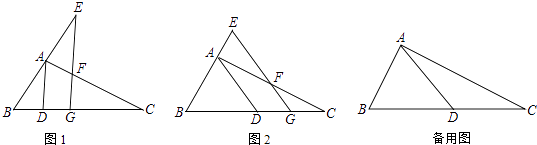
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
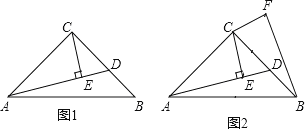
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接BF,
求证:AE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=a(x﹣3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=﹣ ![]() x2﹣2于点B,则A、B两点间的距离为 .
x2﹣2于点B,则A、B两点间的距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣9. 
(1)求证:无论m为何值,该抛物线与x轴总有两个交点;
(2)该抛物线与x轴交于A,B两点,点A在点B的左侧,且OA<OB,与y轴的交点坐标为(0,﹣5),求此抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与x轴的交点为N,若点M是线段AN上的任意一点,过点M作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D,点P是线段MC上一点,且满足MP= ![]() MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com