
【题目】如图,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .给出下列五个结论:①
.给出下列五个结论:①![]() ;②
;②![]() 一定是等腰直角三角形;③
一定是等腰直角三角形;③![]() 一定是等腰三角形;④
一定是等腰三角形;④![]() ;⑤
;⑤![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
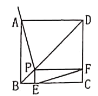
A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
【答案】B
【解析】
连接PC,根据正方形对角线的性质及题中的已知条件,证明△ABP≌△CBP后即可证明AP=PC,再根据矩形对角线相等和角的有关性质即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=![]() EC,也可证明②的正确性,③只在特殊情况下成立.
EC,也可证明②的正确性,③只在特殊情况下成立.
证明:连接PC,
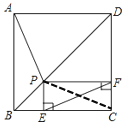
∵点P是正方形ABCD的对角线BD上一点,
∴AB=CB,∠ABP=∠CBP= 45°,BP=BP
∴△ABP≌△CBP,
∴AP=PC,∠BCP=∠BAP,
又∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
∴四边形PECF是矩形,PC=EF且互相平分,
①∴AP=EF正确;∠PFE=∠FEC=∠BCP
∴④∠PFE=∠BAP正确,
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵PF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,即△DPF是等腰直角三角形,即②正确
∵矩形PECF中,PF=EC,
∴在等腰直角三角形△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴⑤DP=![]() EC正确.
EC正确.
∴其中正确结论的序号是①②④⑤.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
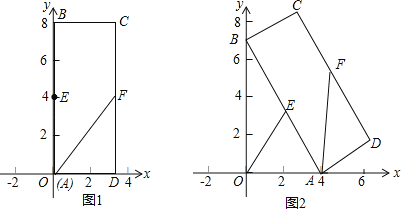
【题目】矩形ABCD中,点C(3,8),E、F为AB、CD边上的中点,如图1,点A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,点B随之沿y轴下滑,并带动矩形ABCD在平面内滑动,如图2,设运动时间表示为t秒,当点B到达原点时停止运动.
(1)当t=0时,点F的坐标为 ;
(2)当t=4时,求OE的长及点B下滑的距离;
(3)求运动过程中,点F到点O的最大距离;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造平安校园,增强学生安全防范意识,某校组织了全校1200名学生参加校园安全网络知识竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | n |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | 0.15 |
80≤x<90 | m | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图.
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 °.
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1200名学生中成绩合格的大约有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5,5![]() ),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;
(3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )
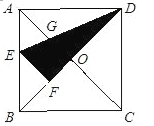
A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
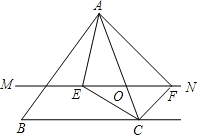
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .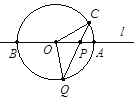
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
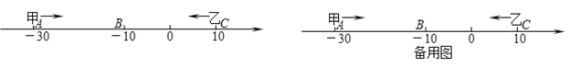
(1)甲,乙经过多少秒在数轴上相遇,并求出相遇点表示的数?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A、B、C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com