
ŅŃÖŖÅ×ĪļĻßy=© x2+bx+cµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1,×īŠ”ÖµĪŖ3£¬“ĖÅ×ĪļĻßÓėyÖį½»ÓŚµćA£¬¶„µćĪŖB£¬¶Ō³ĘÖįBCÓėxÖį½»ÓŚµćC£®
x2+bx+cµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1,×īŠ”ÖµĪŖ3£¬“ĖÅ×ĪļĻßÓėyÖį½»ÓŚµćA£¬¶„µćĪŖB£¬¶Ō³ĘÖįBCÓėxÖį½»ÓŚµćC£®
”¾Š”Ģā1”æ£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½.
”¾Š”Ģā2”æ£Ø2£©ČēĶ¼1£®ĒóµćAµÄ×ų±ź¼°Ļ߶ĪOCµÄ³¤£»
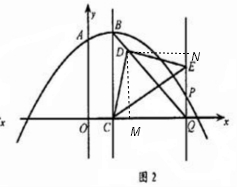
”¾Š”Ģā3”æ£Ø3£©µćPŌŚÅ×ĪļĻßÉĻ£¬Ö±ĻßPQ”ĪBC½»xÖįÓŚµćQ£¬Į¬½ÓBQ£®
¢ŁČōŗ¬45”ć½ĒµÄÖ±½ĒČż½Ē°åČēĶ¼2ĖłŹ¾·ÅÖĆ£®ĘäÖŠ£¬Ņ»øö¶„µćÓėµćCÖŲŗĻ£¬Ö±½Ē¶„µćDŌŚBQÉĻ£¬ĮķŅ»øö¶„µćEŌŚPQÉĻ£®ĒóÖ±ĻßBQµÄŗÆŹż½āĪöŹ½£»
¢ŚČōŗ¬30”ć½ĒµÄÖ±½ĒČż½Ē°åŅ»øö¶„µćÓėµćCÖŲŗĻ£¬Ö±½Ē¶„µćDŌŚÖ±ĻßBQÉĻ£¬ĮķŅ»øö¶„µćEŌŚPQÉĻ£¬ĒóµćPµÄ×ų±ź£®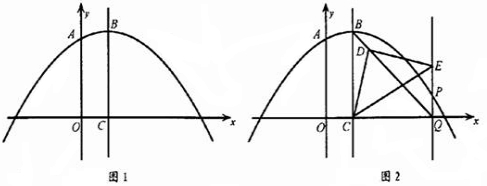
”¾Š”Ģā1”æ½ā£ŗ£Ø1£©”ßÅ×ĪļĻßy=© x2+bx+cµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1
x2+bx+cµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1
”ą2b=1,”ąb=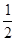
ÓÖ”ßÅ×ĪļĻß×īŠ”ÖµĪŖ3
”ą3=-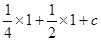 £¬”ąc=
£¬”ąc=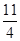
”ąÅ×ĪļĻß½āĪöŹ½ĪŖ£ŗ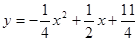
”¾Š”Ģā2”æ2£©°Ńx=0“śČėÅ×ĪļĻßµĆ£ŗy=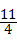 £¬
£¬
”ąµćA£Ø0£¬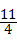 £©£®--------------------------------------3·Ö
£©£®--------------------------------------3·Ö
”ßÅ×ĪļĻߵĶŌ³ĘÖįĪŖx=1£¬
”ąOC=1£®
”¾Š”Ģā3”æ£Ø3£©¢ŁČēĶ¼£ŗ”ß“ĖÅ×ĪļĻßÓėyÖį½»ÓŚµćA£¬¶„µćĪŖB
”ąB£Ø1£¬3£©
·Ö±š¹żµćD×÷DM”ĶxÖįÓŚM£¬DN”ĶPQÓŚµćN£¬
”ßPQ”ĪBC£¬”ą”ĻDMQ=”ĻDNQ=”ĻMQN=90”ć£¬
”ąDMQNŹĒ¾ŲŠĪ£®
”ß”÷CDEŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąDC=DE£¬”ĻCDM=”ĻEDN
”ą”÷CDM”Õ”÷EDN
”ąDM=DN£¬
”ąDMQNŹĒÕż·½ŠĪ£¬
”ą”ĻBQC=45”ć
”ąCQ=CB=3
”ąQ£Ø4£¬0£©
ÉčBQµÄ½āĪöŹ½ĪŖ£ŗy=kx+b£¬
°ŃB£Ø1£¬3£©£¬Q£Ø4£¬0£©“śČė½āĪöŹ½µĆ£ŗk=©1£¬b=4£®
ĖłŅŌÖ±ĻßBQµÄ½āĪöŹ½ĪŖ£ŗy=©x+4£®-------------------------------6·Ö
¢ŚĖłĒóµÄµćPµÄ×ų±źĪŖ£ŗP1£Ø1+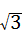 £¬
£¬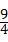 £©£¬P2£Ø1+3
£©£¬P2£Ø1+3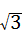 £¬©
£¬©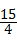 £©£¬P3£Ø1©
£©£¬P3£Ø1©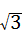 £¬
£¬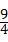 £©£¬
£©£¬
P4£Ø1©3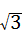 £¬©
£¬©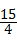 £©£®
£©£®
½āĪö


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| AӢ4 | BӢ8 | CӢ-4 | DӢ16 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 £Ø1£©Ēób+cµÄÖµ£»
£Ø1£©Ēób+cµÄÖµ£»²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 £Ø2012•ŗēæŚĒųŅ»Ä££©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖÅ×ĪļĻßy=x2+bx+c¾¹żA£Ø0£¬3£©£¬B£Ø1£¬0£©Į½µć£¬¶„µćĪŖM£®
£Ø2012•ŗēæŚĒųŅ»Ä££©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖÅ×ĪļĻßy=x2+bx+c¾¹żA£Ø0£¬3£©£¬B£Ø1£¬0£©Į½µć£¬¶„µćĪŖM£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com