
【题目】如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数. 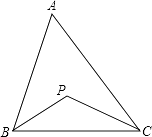
【答案】解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= ![]() (∠ABC+∠ACB)=60°.
(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°﹣60°=120°.
故答案为:120°
【解析】先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠PBC+∠PCB的度数,由三角形内角和定理即可得出结论.
【考点精析】通过灵活运用三角形的内角和外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x和反比例函数 ![]() (k>0),点A(m,n)(m>0)在反比例函数
(k>0),点A(m,n)(m>0)在反比例函数![]() 上.
上.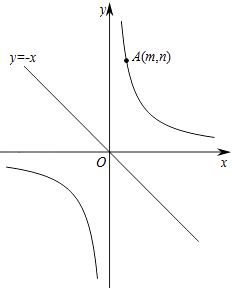
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与反比例函数 ![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与反比例函数 ![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问: ![]() 与
与 ![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列算式:①(a3)2=a3×2=a6;②aman=am+n(m,n为正整数);③[(-x)4]5=-x20.其中正确的算式有( ).
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m+a=n+b,根据等式性质变形为m=n,那么a,b必须符合的条件是( )
A.a=﹣b
B.﹣a=b
C.a=b
D.a,b可以是任意有理数或整式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(﹣1,﹣2),将OA绕原点O逆时针旋转180°得到OA′,点A′的坐标为(a,b),则a﹣b等于( )
A.1
B.﹣1
C.3
D.﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com