
已知点E 、F
、F 在抛物线
在抛物线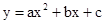 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
 的数量关系式为:S=
的数量关系式为:S= 
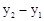 .
.
解析试题分析:首先根据题意可求得:y1,y2的值,A与C的坐标,即可用x1与x2表示出AB,CD,BD的值,易得四边形ABCD是直角梯形,即可得S=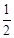 (AB+CD)•BD,然后代入其取值,整理变形,即可求得S与y1、y2的数量关系式:
(AB+CD)•BD,然后代入其取值,整理变形,即可求得S与y1、y2的数量关系式:
根据题意得: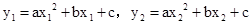 ,
,
∵点A、C在直线y=2ax+b上,∴点A的坐标为:(x1,2ax1+b),点C的坐标为:(x2,2ax2+b).
∴AB=2ax1+b,CD=2ax2+b,BD=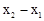 .
.
∵EB⊥BD,CD⊥BD,∴AB∥CD. ∴四边形ABCD是直角梯形.
∴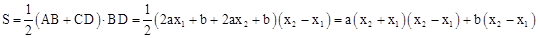
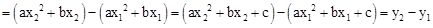
∴S与y1、y2的数量关系式为:S=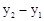 .
.
考点:1.二次函数综合题;2.曲线上点的坐标与方程的关系;3. 直角梯形的判定和性质.


科目:初中数学 来源: 题型:填空题
如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,一段抛物线
 与
与 轴交于点
轴交于点 ,
, ;将
;将 向右平移得第2段抛物线
向右平移得第2段抛物线 ,交
,交 轴于点
轴于点 ;再将
;再将 向右平移得第3段抛物线
向右平移得第3段抛物线 ,交
,交 轴于点
轴于点 ;又将
;又将 向右平移得第4段抛物线
向右平移得第4段抛物线 ,交
,交 轴于点
轴于点 ,若
,若 在
在 上,则
上,则 的值是 .
的值是 .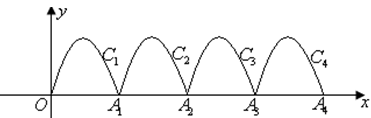
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是 千米.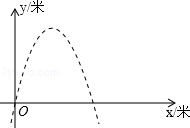
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线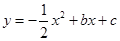 图象经过A(-1,0),B(4,0)两点.
图象经过A(-1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.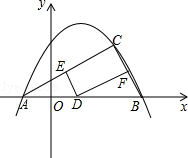
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com