
分析 (1)观察不难发现,相邻的两个数,后面的数比前面的数大5,然后依次写出即可;
(2)由已知发现分母依次为:23,24,25,26,27;分子为:2,3,4,5,6,7;符号为“+-+-+-”,由此可知结果.
解答 解:(1)-23,-18,-13,-8,-3.
故答案为:-8,-3;
(2)由已知发现分母依次为:23,24,25,26,27;
分子为:2,3,4,5,6,7;
所以两个数依次为:$\frac{6}{128}$,-$\frac{7}{256}$,
故答案为:$\frac{6}{128}$,$-\frac{7}{256}$.
点评 本题主要考查了数字的变化规律,发现分子分母及符号的变化规律是解答此题的关键.


科目:初中数学 来源: 题型:解答题
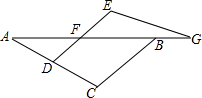 甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com