
【题目】综合题。
(1)解方程:x2=2x.
(2)如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC向右平移至△A′B′C′的位置,使得四边形ABB′A′为菱形,求B′C的长. 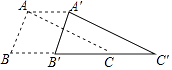
【答案】
(1)解:∵x2﹣2x=0,
∴x(x﹣2)=0,
则x=0或x=2;
(2)解:∵∠BAC=90°,AB=5,AC=12,
∴BC= ![]() =
= ![]() =13,
=13,
∵四边形ABB′A′为菱形,
∴BB′=AB=5,
则B′C=BC﹣BB′=13﹣5=8.
【解析】(1)因式分解法求解可得;(2)根据勾股定理求得BC=13,根据菱形的性质得BB′=5,即可得答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB; 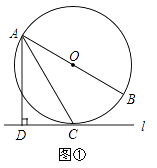
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF. 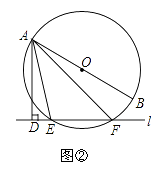
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( ) 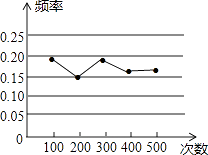
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE. 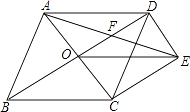
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
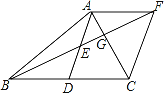
【题目】如图,AD是△ABC的边BC的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF,BF交AC于G.
(1)若四边形ADCF是菱形,试证明△ABC是直角三角形;
(2)求证:CG=2AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算: 
(1)若小明随机选择一个插座插入,则插入A的概率为;
(2)现小明对手机和学习机两种电器充电,请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况,并计算两个插头插在相邻插座的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果,矩形ABCD中,点E在AB上,点F在CD上,点G,H在对角线AC上,且CH=AG,CF=AE. 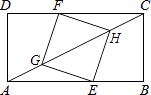
(1)求证:△AGE≌△CHF;
(2)若AB=8,AD=4,且GH恰好平分∠FGE,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF. 
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com