
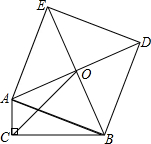
 如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC.
如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC.
|
| AC+BC |
| 2 |
| 2 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
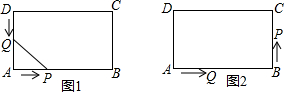 如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 “囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可)
如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com