
【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足 ![]() +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处. 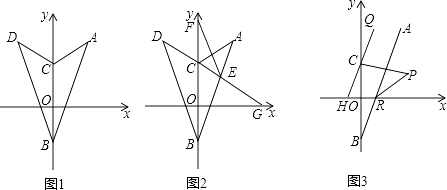
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
【答案】
(1)解:∵ ![]() +(n﹣5)2=0,
+(n﹣5)2=0,
∴m+5=0,n﹣5=0,
∴m=﹣5,n=5,
∴A点坐标为(5,5),
∵△ABC沿y轴折叠,使点A落在点D处,
∴点D与点A关于y轴对称,
∴D点坐标为(﹣5,5);
∴AD=5﹣(﹣5)=10
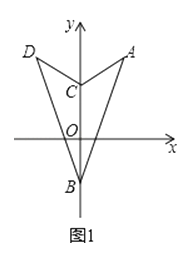
(2)解:如图2,∵△ABC沿x轴折叠,使点A落在点D处,
∴∠DCF=∠ACF,
∵∠DCF=∠EFB+∠DEF,
∴∠EFB=∠ACF﹣∠DEF,
∵EF平分∠AED,
∴∠DEF=∠AEF,
∴∠EFB=∠ACF﹣∠AEF=20°
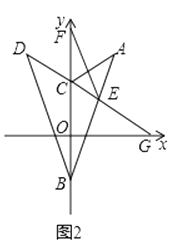
(3)解:∠CPH=45°.理由如下:
如图3,∵QH∥AB,
∴∠QCP=∠1,∠ARX=∠3,
∵CP、RP分别平分∠BCQ和∠ARX,
∴∠QCP= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠ARX,
∠ARX,
∴∠1= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠3,
∠3,
∵∠BCQ=90°+∠3,
∴2∠1=90°+2∠2,即∠1=45°+∠2,
∵∠1=∠CPR+∠2,
∴∠CPR=45°
【解析】(1)先由非负数的性质求出m,n的值,得到A点坐标,再根据折叠的性质得点D与点A关于y轴对称,再根据关于y轴对称的点的坐标特征得到D点坐标,然后计算点A与点D的横坐标之差即可得到A、D两点间的距离;(2)根据折叠的性质得∠DCF=∠ACF,再利用三角形外角性质得∠DCF=∠EFB+∠DEF,则∠EFB=∠ACF﹣∠DEF,又∠DEF=∠AEF,所以∠EFB=∠ACF﹣∠AEF=20°;(3)根据平行线的性质由QH∥AB得到∠QCP=∠1,∠ARX=∠3,再根据角平分线的定义得∠QCP= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠ARX,则∠1=
∠ARX,则∠1= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠3,接着利用三角形外角性质得∠BCQ=90°+∠3,所以2∠1=90°+2∠2,即∠1=45°+∠2,然根据∠1=∠CPR+∠2即可得到∠CPR=45°.
∠3,接着利用三角形外角性质得∠BCQ=90°+∠3,所以2∠1=90°+2∠2,即∠1=45°+∠2,然根据∠1=∠CPR+∠2即可得到∠CPR=45°.
【考点精析】通过灵活运用三角形的内角和外角和三角形的外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 有一个角是直角的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直平分的四边形是正方形
D. 两条对角线相等的菱形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.求:
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台用如下图所示的图像向观察描绘了一周之内日平均温度的变化情况:

(1)这一周哪一天的日平均温度最低?大约是多少度?哪一天的平均温度最高?大约是多少度?你能用有序数对分别表示它们吗?
(2)14、15、16日的日平均温度有什么关系?
(3)说一说这一周日平均温度是怎样变化的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:
![]() ________,
________, ![]() ________,
________, ![]() ________;
________;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:________;
经过怎样的平移得到:________;
(3)若点 ![]() (
( ![]() ,
,![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点 ![]() 的坐标为________;
的坐标为________;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全等图形是相似比为1的相似图形,因此全等是特殊的相似,我们可以由研究全等三角形的思路,提出相似三角形的问题和研究方法.这种其中主要利用的数学方法是( )
A.代入法B.列举法C.从特殊到一般D.反证法
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com