
分析 (1)观察已知等式得出一般性规律,写出即可;
(2)原式利用得出的规律变形,约分即可得到结果.
解答 解:(1)1-$\frac{1}{10{0}^{2}}$=$\frac{99}{100}$×$\frac{101}{100}$;1-$\frac{1}{200{9}^{2}}$=$\frac{2008}{2009}$×$\frac{2010}{2009}$;
故答案为:$\frac{99}{100}$;$\frac{101}{100}$;$\frac{2008}{2009}$;$\frac{2010}{2009}$;
(2)原式=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×…×$\frac{2008}{2009}$×$\frac{2010}{2009}$×$\frac{2009}{2010}$×$\frac{2011}{2010}$=$\frac{1}{2}$×$\frac{2011}{2010}$=$\frac{2011}{4020}$.
点评 此题考查了有理数的混合运算,观察已知等式得出一般性规律是解本题的关键.


科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是正方形,以B点为圆心,BD的长为半径画弧交BC延长线于点E,以DE为边作正方形DEFG,作FH⊥BE交BE的延长线于点H,连接AE、CG,则下列结论中正确的有( )
如图,四边形ABCD是正方形,以B点为圆心,BD的长为半径画弧交BC延长线于点E,以DE为边作正方形DEFG,作FH⊥BE交BE的延长线于点H,连接AE、CG,则下列结论中正确的有( )| A. | ①②③④⑤ | B. | ①②③④ | C. | ①②③ | D. | ①②③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
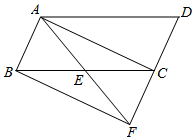 如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
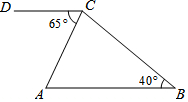 如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )| A. | 105° | B. | 95° | C. | 85° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com