
【题目】为鼓励下岗工人再就业,某地市政府规定,企业按成本价提供产品给下岗人员自主销售,成本价与出厂价之间的差价由政府承担.老李按照政策投资销售本市生产的一种儿童面条.已知这种儿童面条的成本价为每袋12元,出厂价为每袋16元,每天销售量![]() (袋)与销售单价
(袋)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)老李在开始创业的第1天将销售单价定为17元,那么政府这一天为他承担的总差价为多少元?
(2)设老李获得的利润为![]() (元),当销售单价为多少元时,每天可获得最大利润?
(元),当销售单价为多少元时,每天可获得最大利润?
(3)物价部门规定,这种面条的销售单价不得高于24元,如果老李想要每天获得的利润不低于216元,那么政府每天为他承担的总差价最少为多少元?
【答案】(1)政府这个月为承担的总差价为156元;(2)当销售单价定为21元时,每月可获得最大利润243元;(3)销售单价定为24元时,政府每个月为他承担的总差价最少为72元.
【解析】
(1)把x=17代入y=3x+90求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由总利润=销售量每件纯赚利润,得![]() ,把函数转化成顶点坐标式,根据二次函数的性质求出销售单价及最大利润;
,把函数转化成顶点坐标式,根据二次函数的性质求出销售单价及最大利润;
(3)令![]() ,求出x的值,求出利润的范围,然后根据一次函数的性质求出总差价的最小值.
,求出x的值,求出利润的范围,然后根据一次函数的性质求出总差价的最小值.
解:(1)当![]() 时,
时,![]() ,
,
![]() ,即政府这个月为承担的总差价为156元;
,即政府这个月为承担的总差价为156元;
(2)依题意得,![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最大值243,
有最大值243,
即当销售单价定为21元时,每月可获得最大利润243元;
(3)由题意得:![]() ,解得:
,解得:![]() ,
,
∵![]() ,抛物线开口向下,
,抛物线开口向下,
∴当![]() 时,
时,![]() ,
,
设政府每个月为他承担的总差价为![]() 元,
元,
∴![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 最小
最小![]() ,
,
即销售单价定为24元时,政府每个月为他承担的总差价最少为72元.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
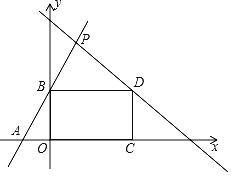
A.(2,8)B.![]() C.
C.![]() D.(4,12)
D.(4,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
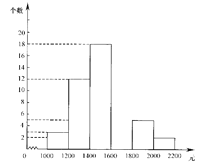
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
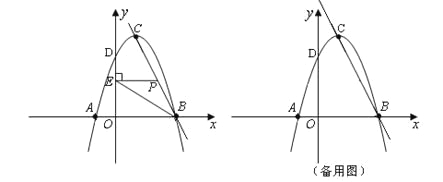
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
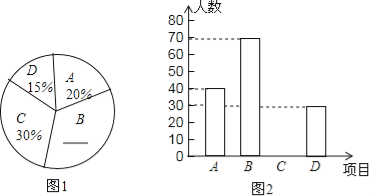
(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给抛物线y=a(x﹣h)2+k(a≠0)定义一种变换,先作这条抛物线关于原点对称的抛物线![]() ,再将得到的对称抛物线
,再将得到的对称抛物线![]() 向上平移m(m>0)个单位长度,得到新的抛物线ym,则我们称ym为二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.若抛物线M的6阶变换的关系式为
向上平移m(m>0)个单位长度,得到新的抛物线ym,则我们称ym为二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.若抛物线M的6阶变换的关系式为![]() .
.
(1)抛物线M的函数表达式为 ;
(2)若抛物线M的顶点为点A,与r轴相交的两个交点中的左侧交点为点B,则在抛物线![]() 上是否存在点P,使点P与直线AB的距离最短?若存在,请求出此时点P的坐标.
上是否存在点P,使点P与直线AB的距离最短?若存在,请求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
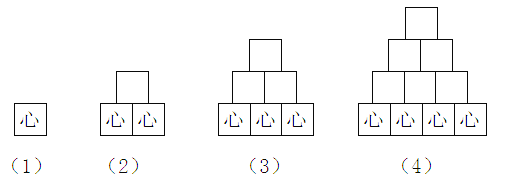
【题目】小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体,……按照此规律,从第(100)个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com