
(10分) 1.(1)如图1,已知点P在正三角形ABC的边BC上,以AP为边作正三角形APQ,连接
CQ.

①求证:△ABP≌△ACQ;
②若AB=6,点D是AQ的中点,直接写出当点P由点B运动到点C时,点D运动路线的
长.
2.(2)已知,△EFG中,EF=EG=13,FG=10.如图2,把△EFG绕点E旋转到△EF'G'的位置,点M是边EF'与边FG的交点,点N在边EG'上且EN=EM,连接GN.
求点E到直线GN的距离.
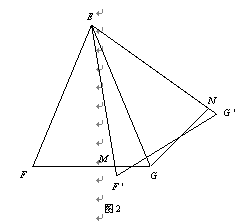
(1)①因为三角形ABC和三角形APQ是正三角形,
所以AB=AC,AP=AQ,∠BAC=∠PAQ.
所以∠BAC-∠PAC=∠PAQ-∠PAC.
所以∠BAP=∠CAQ.
所以△ABP≌△ACQ.……………………3分
②3……………………5分
1.
2. (2)解法一:
(2)解法一:
过点E作底边FG的垂线,点H为垂足.
在△EFG中,易得EH=12.……………………6分
类似(1)可证明△EFM≌△EGN,……………………7分
所以∠EFM=∠EGN.
因为∠EFG=∠EGF,
所以∠EGF=∠EGN,
所以GE是∠FGN的角平分线,……………………9分
所以点E到直线FG和GN的距离相等,
所以点E到直线GN的距离是12.……………10分
解法二:
 过点E作底边FG的垂线,点H为垂足.过点E作直线
过点E作底边FG的垂线,点H为垂足.过点E作直线
GN的垂线,点K为垂足.
在△EFG中,易得EH=12.……………………6分
类似(1)可证明△EFM≌△EGN,……………………7分
所以,∠EFM=∠EGN.
可证明△EFH≌△EGK,……………………9分
所以,EH=EK.
所以点E到直线GN的距离是12.………………10分
解法三:
 把△EFG绕点E旋转,对应着点M在边FG上从点F开始运动.
把△EFG绕点E旋转,对应着点M在边FG上从点F开始运动.
由题意,在运动过程中,点E到直线GN的距离不变.
不失一般性,设∠EMF=90°.
类似(1)可证明△EFM≌△EGN,
所以,∠ENG=∠EMF=90°.
求得EM=12.
所以点E到直线GN的距离是12.
(酌情赋分)
解析:略


科目:初中数学 来源: 题型:
| 甲、乙两县成绩统计表 | 乙县成绩扇形统计图 | ||||
| 分数 | 7分 | 8分 | 9分 | 10分 |  |
| 甲县人数 | 11 | 1 | 0 | 8 | |
| 乙县人数 | 8 | 3 | 5 | ||
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com