
”¾ĢāÄæ”æijĘū³µŌŚÉ²³µŗóŠŠŹ»µÄ¾ąĄės(µ„Ī»£ŗĆ×)ÓėŹ±¼ät(µ„Ī»£ŗĆė)Ö®¼äµÄ¹ŲĻµµĆ²æ·ÖŹż¾ŻČēĻĀ±ķ£ŗ
Ź±¼ät(Ćė) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | ” |
ŠŠŹ»¾ąĄės(Ć×) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | ” |
¼ŁÉčÕāÖÖ±ä»Æ¹ęĀÉŅ»Ö±ŃÓŠųµ½Ęū³µĶ£Ö¹£®
(1)øł¾ŻÕāŠ©Źż¾ŻŌŚøų³öµÄ×ų±źĻµÖŠ»³öĻąÓ¦µÄµć£»
(2)Ń”ŌńŹŹµ±µÄŗÆŹż±ķŹ¾sÓėtÖ®¼äµÄ¹ŲĻµ£¬Ēó³öĻąÓ¦µÄŗÆŹż½āĪöŹ½£»
(3)¢ŁÉ²³µŗóĘū³µŠŠŹ»ĮĖ¶ą³¤¾ąĄė²ÅĶ£Ö¹?
¢Śµ±t·Ö±šĪŖt1,t2(t1<t2)Ź±,¶ŌÓ¦sµÄÖµ·Ö±šĪŖs1,s2,Ēė±Č½Ļ![]() Óė
Óė![]() µÄ“󊔣®
µÄ“󊔣®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©![]() £»£Ø3£©¢Ł
£»£Ø3£©¢Ł![]() Ć×£»¢Ś
Ć×£»¢Ś![]() £¾
£¾![]()
”¾½āĪö”æ
£Ø1£©Ćčµć£¬ÓĆĘ½»¬ĒśĻßĮ¬½Ó¼“æÉ£»
£Ø2£©Éč³ö¶ž“ĪŗÆŹż½āĪöŹ½£¬°Ń3øöµćµÄ×ų±ź“śČėæɵƶž“ĪŗÆŹż½āĪöŹ½£¬½ų¶ųŌŁ°ŃĘäÓąµÄµć“śČėŃéÖ¤ŹĒ·ńŌŚ¶ž“ĪŗÆŹżÉĻ£»
£Ø3£©¢ŁĘū³µŌŚÉ²³µŹ±¼ä×ī³¤Ź±Ķ£Ö¹£¬ĄūÓĆ¹«Ź½·Ø£¬½įŗĻ£Ø2£©µĆµ½µÄŗÆŹż½āĪöŹ½£¬ĒóµĆĻąÓ¦µÄ×īÖµ¼“æÉ£»
¢Ś·Ö±šĒóµĆĖłøų“śŹżŹ½µÄÖµ£¬øł¾ŻĖłøųŹ±¼äµÄ“󊔣¬±Č½Ļ¼“æÉ£®
(1)ĆčµćĶ¼ĖłŹ¾£ŗ
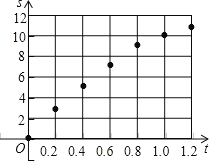
(2)ÓÉÉ¢µćĶ¼æÉÖŖøĆŗÆŹżĪŖ¶ž“ĪŗÆŹż
É趞“ĪŗÆŹżµÄ½āĪöŹ½ĪŖ£ŗs=at2+bt+c£¬
”ßÅ×ĪļĻß¾¹żµć(0,0)£¬
”ąc=0£¬
ÓÖÓɵć(0.2,2.8),(1,10)æÉµĆ£ŗ
![]()
½āµĆ£ŗa=5£¬b=15£»
”ą¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖ£ŗs=5t2+15t£»
¾¼ģŃé,ĘäÓąø÷µć¾łŌŚs=5t2+15tÉĻ.
(3)¢ŁĘū³µÉ²³µŗóµ½Ķ£Ö¹Ź±µÄ¾ąĄė¼“Ęū³µ»¬ŠŠµÄ×ī“ó¾ąĄė£¬
µ±t=![]() =
=![]() Ź±,»¬ŠŠ¾ąĄė×ī“ó,S=
Ź±,»¬ŠŠ¾ąĄė×ī“ó,S=![]() =
=![]() =
=![]() £¬
£¬
¼“ɲ³µŗóĘū³µŠŠŹ»ĮĖ![]() ĆײÅĶ£Ö¹.
ĆײÅĶ£Ö¹.
¢Ś”ßs=5t2+15t,
”ą![]() ,
,![]()
”ą![]()
Ķ¬Ąķ![]() £¬
£¬
”ßt1<t2£¬
”ą![]() £¾
£¾![]()



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(1)![]()
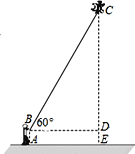
(2)ČēĶ¼£¬Š”·½ŌŚĒåĆ÷¼ŁĘŚÖŠµ½½¼Ķā·Å·ēóŻ£¬·ēóŻ·Éµ½C “¦Ź±µÄĻß³¤BCĪŖ20Ć×£¬“ĖŹ±Š”·½ÕżŗĆÕ¾ŌŚA“¦£¬²¢²āµĆ”ĻCBD=60”ć£¬Ē£Ņżµ×¶ĖBĄėµŲĆę1.5Ć×£¬Ēó“ĖŹ±·ēóŻĄėµŲĆęµÄø߶Č.(![]() ,
,![]() £¬½į¹ū¾«Č·µ½0.1Ć×)
£¬½į¹ū¾«Č·µ½0.1Ć×)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚRt”÷ABCÖŠ£¬DĪŖŠ±±ßABµÄÖŠµć£¬”ĻB=60”ć£¬BC=2cm£¬¶ÆµćE“ÓµćA³ö·¢ŃŲABĻņµćBŌĖ¶Æ£¬¶ÆµćF“ÓµćD³ö·¢£¬ŃŲÕŪĻßD©C©BŌĖ¶Æ£¬Į½µćµÄĖŁ¶Č¾łĪŖ1cm/s£¬µ½“ļÖÕµć¾łĶ£Ö¹ŌĖ¶Æ£¬ÉčAEµÄ³¤ĪŖx£¬”÷AEFµÄĆ껿ĪŖy£¬ŌņyÓėxµÄĶ¼Ļó“óÖĀĪŖ£Ø””””£©

A.  B.
B. 
C.  D.
D. 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö²»ĶøĆ÷µÄ²¼“üĄļ×°ÓŠ2øö°×Ēņ£¬1øöŗŚĒņŗĶČōøÉøöŗģĒņ£¬ĖüĆĒ³żŃÕÉ«ĶāĘäÓą¶¼ĻąĶ¬£¬“ÓÖŠČĪŅāĆž³ö1øöĒņ£¬ŹĒŗģĒņµÄøÅĀŹĪŖ![]() £®
£®
£Ø1£©²¼“üĄļŗģĒņÓŠ______øö.
£Ø2£©ĻČ“Ó²¼“üÖŠĆž³öøöĒņŗó²»·Å»Ų£¬ŌŁĆž³ö1øöĒņ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒó³öĮ½“ĪĆžµ½µÄĒņ¶¼ŹĒ°×ĒņµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
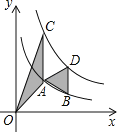
”¾ĢāÄæ”æČēĶ¼£¬µćA£¬BŌŚ·“±ČĄżŗÆŹży£½![]() (x£¾0)µÄĶ¼ĻóÉĻ£¬µćC£¬DŌŚ·“±ČĄżŗÆŹży£½
(x£¾0)µÄĶ¼ĻóÉĻ£¬µćC£¬DŌŚ·“±ČĄżŗÆŹży£½![]() (k£¾0)µÄĶ¼ĻóÉĻ£¬AC”ĪBD”ĪyÖį£¬ŅŃÖŖµćA£¬BµÄŗį×ų±ź·Ö±šĪŖ1£¬2£¬”÷OACÓė”÷ABDµÄĆ껿֮ŗĶĪŖ
(k£¾0)µÄĶ¼ĻóÉĻ£¬AC”ĪBD”ĪyÖį£¬ŅŃÖŖµćA£¬BµÄŗį×ų±ź·Ö±šĪŖ1£¬2£¬”÷OACÓė”÷ABDµÄĆ껿֮ŗĶĪŖ![]() £¬ŌņkµÄÖµĪŖ_____£®
£¬ŌņkµÄÖµĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() ÓėxÖį½»ÓŚµćA£¬B£¬Óė
ÓėxÖį½»ÓŚµćA£¬B£¬Óė![]() Öį½»ÓŚµćC”£¹żµćC×÷CD”ĪxÖį£¬½»Å×ĪļĻߵĶŌ³ĘÖįÓŚµćD£¬Į¬½įBD”£ŅŃÖŖµćA×ų±źĪŖ£Ø-1£¬0£©”£
Öį½»ÓŚµćC”£¹żµćC×÷CD”ĪxÖį£¬½»Å×ĪļĻߵĶŌ³ĘÖįÓŚµćD£¬Į¬½įBD”£ŅŃÖŖµćA×ų±źĪŖ£Ø-1£¬0£©”£

£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ĒóĢŻŠĪCOBDµÄĆ껿”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() £Ø
£Ø![]() ŹĒ³£Źż£¬
ŹĒ³£Źż£¬ ![]() £©£®
£©£®
£Ø![]() £©µ±øĆŗÆŹżµÄĶ¼ĻńÓė
£©µ±øĆŗÆŹżµÄĶ¼ĻńÓė![]() Öįƻӊ½»µćŹ±£¬Ēó
Öįƻӊ½»µćŹ±£¬Ēó![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
£Ø![]() £©°ŃøĆŗÆŹżµÄĶ¼ĻńŃŲ
£©°ŃøĆŗÆŹżµÄĶ¼ĻńŃŲ![]() ÖįĻņÉĻĘ½ŅʶąÉŁøöµ„Ī»³¤¶Čŗó£¬µĆµ½µÄŗÆŹżµÄĶ¼ĻńÓė
ÖįĻņÉĻĘ½ŅʶąÉŁøöµ„Ī»³¤¶Čŗó£¬µĆµ½µÄŗÆŹżµÄĶ¼ĻńÓė![]() ÖįÖ»ÓŠŅ»øö¹«¹²µć£æ
ÖįÖ»ÓŠŅ»øö¹«¹²µć£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŹĒ”ŃOµÄÄŚ½ÓČż½ĒŠĪ£¬ABŹĒ”ŃOµÄÖ±¾¶£¬OF”ĶAB£¬½»ACÓŚµćF£¬µćEŌŚABµÄŃÓ³¤ĻßÉĻ£¬ÉäĻßEM¾¹żµćC£¬ĒŅ”ĻACE+”ĻAFO=180”ć.
£Ø1£©ĒóÖ¤£ŗEMŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ĻA=”ĻE,BC=![]() £¬ĒóŅõÓ°²æ·ÖµÄĆ껿.£Ø½į¹ū±£Įō
£¬ĒóŅõÓ°²æ·ÖµÄĆ껿.£Ø½į¹ū±£Įō![]() ŗĶøłŗÅ£©.
ŗĶøłŗÅ£©.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ¼Ņ¾ĻśŅ»ÖÖĀĢ²č£¬ÓĆӌװŠŽĆÅĆęŅŃĶ¶×Ź4000ŌŖŅŃÖŖĀĢ²čĆæĒ§æĖ³É±¾40ŌŖ£¬¾ŃŠ¾æ·¢ĻÖĻśĮæy£Økg£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ/kg£©Ö®¼äµÄŗÆŹż¹ŲĻµŹĒ![]() £Ø
£Ø![]() £©£®ŅŌøĆĀĢ²čµÄŌĀĻśŹŪĄūČóĪŖw£ØŌŖ£©[ĻśŹŪĄūČó
£©£®ŅŌøĆĀĢ²čµÄŌĀĻśŹŪĄūČóĪŖw£ØŌŖ£©[ĻśŹŪĄūČó![]() £ØĆæĒ§æĖµ„¼Ū
£ØĆæĒ§æĖµ„¼Ū![]() ĆæĒ§æĖ³É±¾£©
ĆæĒ§æĖ³É±¾£©![]() ĻśŹŪĮæ]
ĻśŹŪĮæ]
£Ø1£©ĒómÓėÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öxĪŖŗĪÖµŹ±£¬wµÄÖµ×ī“ó£æ
£Ø2£©ČōŌŚµŚŅ»øöŌĀĄļ£¬°“Ź¹w»ńµĆ×ī“óÖµµÄĻśŹŪµ„¼Ū½ųŠŠĻśŹŪŗó£¬ŌŚµŚ¶žøöŌĀĄļŹÜĪļ¼Ū²æĆÅøÉŌ¤£¬ĻśŹŪµ„¼Ū²»µĆøßÓŚ85ŌŖ£¬ŅŖĻėŌŚČ«²æŹÕ»ŲĶ¶×ŹµÄ»ł“”ÉĻŹ¹µŚ¶žøöŌĀµÄĄūČó“ļµ½2200ŌŖ£¬ÄĒĆ“µŚ¶žøöŌĀĄļÓ¦øĆČ·¶ØĻśŹŪµ„¼ŪĪŖ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com