
【题目】某校兴趣小组在创客嘉年华活动中组织了计算机编程比赛,八年级每班派25名学生参加,成绩分别为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
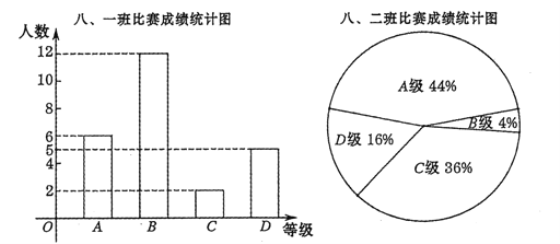
班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
一班 | 8.76 | 9 | 9 |
|
二班 | 8.76 | 8 | 10 |
|
请根据本学期所学过的《数据的分析》相关知识分析上述数据,帮助计算机编程老师选择一个班级参加校级比赛,并阐述你选择的理由.
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
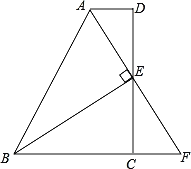
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
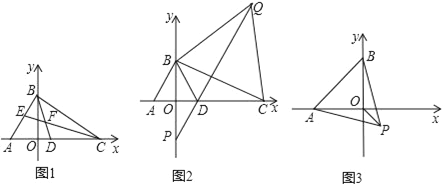
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
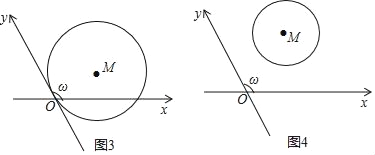
【题目】我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系,如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系,两条数轴称为斜坐标系的坐标轴,公共原点称为斜坐标系的原点,如图1,经过平面内一点P作坐标轴的平行线PM和PN,分别交x轴和y轴于点M,N.点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标,有序实数对(x,y)称为点P的斜坐标,记为P(x,y).
(1)如图2,ω=45°,矩形OABC中的一边OA在x轴上,BC与y轴交于点D,OA=2,OC=l.
①点A、B、C在此斜坐标系内的坐标分别为A ,B ,C .
②设点P(x,y)在经过O、B两点的直线上,则y与x之间满足的关系为 .
③设点Q(x,y)在经过A、D两点的直线上,则y与x之间满足的关系为 .
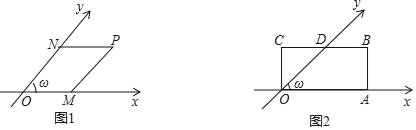
(2)若ω=120°,O为坐标原点.
①如图3,圆M与y轴相切原点O,被x轴截得的弦长OA=4![]() ,求圆M的半径及圆心M的斜坐标.
,求圆M的半径及圆心M的斜坐标.
②如图4,圆M的圆心斜坐标为M(2,2),若圆上恰有两个点到y轴的距离为1,则圆M的半径r的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-3,3),B(-4,-2),C(-1,-1).
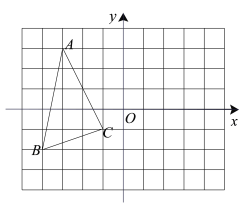
(1)在图中作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标________;
(2)在y轴上画出点P,使PA+PC最小,并直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() .
.

(1)![]() 点的坐标为( , ),
点的坐标为( , ),![]() 点的坐标为( , );
点的坐标为( , );
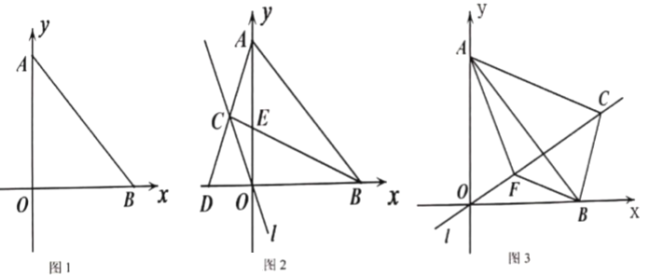
(2)如图1,已知直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,点
,点![]() 在直线AB上且位于
在直线AB上且位于![]() 轴右侧图象上一点,连接
轴右侧图象上一点,连接![]() ,且
,且![]()
![]() .
.
①求![]() 点坐标;
点坐标;
②将![]() 沿直线AM 平移得到
沿直线AM 平移得到![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合,
重合,![]() 为
为![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出最小值及此时 N 点的坐标;
的值最小时,请求出最小值及此时 N 点的坐标;
(3)如图 2,将点![]() 向左平移 2 个单位到点
向左平移 2 个单位到点![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 经过点
经过点![]() 和点
和点![]() ,动点
,动点![]() 从原点出发沿着
从原点出发沿着![]() 轴正方向运动,连接
轴正方向运动,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 、
、![]() ,且
,且![]() 、
、![]() 满足
满足![]()
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过点![]() 的直线
的直线![]() 上有一点
上有一点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,如图2,当点
,如图2,当点![]() 在第二象限时,
在第二象限时,![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,如图3,当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com