
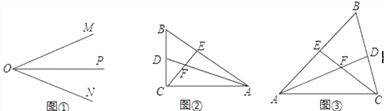
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.
【答案】(1)画图见解析;(2)DF=EF,理由见解析;(3)DF=EF 仍然成立,理由见解析.
【解析】(1)在∠MON的两边上以O为端点截取相等的两条相等的线段,两个端点与角平分线上任意一点相连,所构成的两个三角形全等,即△COB≌△AOB;
(2)根据图(1)的作法,在CG上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据图(1)的作法,在CG上截取AG=AE,证得△EAF≌△GAF(SAS),得出FE=FG;再根据ASA证明△FDC≌△FGC,得DF=FG,故得出EF=FD.
解:(1)如图①所示,△COB≌△AOB,点C即为所求.
(2)如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
CG=CD,∠DCF=∠GCF,CF=CF,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,且∠EAF=∠GAF,
∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() =60°,
=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
∠AFE=∠AFG,AF=AF,∠EAF=∠GAF,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=60°,
(∠BAC+∠ACB)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.

“点睛”此题主要考查全等三角形的判定和性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.


科目:初中数学 来源: 题型:
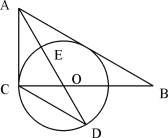
【题目】如图,在Rt△ABC中,∠ACB=90,AO是△ABC的角平分线。以O为圆心,OC为半径作⊙O。
(1)(3分)求证:AB是⊙O的切线。
(2)(3分)已知AO交⊙O于点E,延长AO交⊙O于点D, tanD=![]() ,求
,求![]() 的值。
的值。
(3)(4分)在(2)的条件下,设⊙O的半径为3,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是( )
A.1cm,2cm,3cmB.2cm,3cm,4cmC.5cm,6cm,12cmD.2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的进价为150元,出售时标价为225元,由于销售情况不好,商店准备降价出售,但要保证利润不低于10%,如果商店要降x元出售此商品,请列出不等式_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD∥BC,当满足下列条件时,四边形ABCD是平行四边形的是( ).
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() 是关于
是关于![]() 的方程
的方程![]() 的解,求
的解,求![]() 的值.
的值.
(2)已知关于x的方程![]() 的解与方程
的解与方程![]() 的解互为倒数,求
的解互为倒数,求![]() 的值.
的值.
(3)小丽在解关于![]() 的方程
的方程![]() 时,出现了一个失误:“在将
时,出现了一个失误:“在将![]() 移到方程的左边时,忘记了变号.”结果她得到方程的解为
移到方程的左边时,忘记了变号.”结果她得到方程的解为![]() ,求
,求![]() 的值和原方程的解.
的值和原方程的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com