练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2004•扬州）下列各式的计算结果是a6的是（ ）
    A．（-a3）2
    B．（-a2）3
    C．a3+a3
    D．a2•a3
    【答案】分析：根据幂的乘方、同底数幂的乘法的运算法则计算后利用排除法求解．
    解答：解：A、（-a3）2=a6，符合；
    B、（-a2）3=-a6，不符合；
    C、a3+a3=2a3，不符合；
    D、a2•a3=a5，不符合．
    故选A．
    点评：本题考查了合并同类项、同底数幂的乘法、幂的乘方，需熟练掌握且区分清楚，才不容易出错．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2004年全国中考数学试题汇编《二次函数》（04）（解析版） 题型：解答题

    （2004•扬州）如图，直角坐标系中，已知点A（3，0），B（t，0）（0＜t＜），以AB为边在x轴上方作正方形ABCD，点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点，连接AE与BC相交于点F．
    （1）求证：△OBC≌△FBA；?
    （2）一抛物线经过O、F、A三点，试用t表示该抛物线的解析式；?
    （3）设题（2）中抛物线的对称轴l与直线AF相交于点G，若G为△AOC的外心，试求出抛物线的解析式；?
    （4）在题（3）的条件下，问在抛物线上是否存在点P，使该点关于直线AF的对称点在x轴上？若存在，请求出所有这样的点；若不存在，请说明理由．

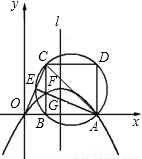
    查看答案和解析>>

    科目：初中数学 来源：2004年江苏省扬州市中考数学试卷（解析版） 题型：解答题

    （2004•扬州）如图，直角坐标系中，已知点A（3，0），B（t，0）（0＜t＜），以AB为边在x轴上方作正方形ABCD，点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点，连接AE与BC相交于点F．
    （1）求证：△OBC≌△FBA；?
    （2）一抛物线经过O、F、A三点，试用t表示该抛物线的解析式；?
    （3）设题（2）中抛物线的对称轴l与直线AF相交于点G，若G为△AOC的外心，试求出抛物线的解析式；?
    （4）在题（3）的条件下，问在抛物线上是否存在点P，使该点关于直线AF的对称点在x轴上？若存在，请求出所有这样的点；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2004年全国中考数学试题汇编《图形的对称》（03）（解析版） 题型：解答题

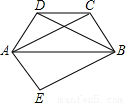
    （2004•扬州）如图，在等腰梯形ABCD中，AB∥CD，AC、BD是对角线，将△ABD沿AB向下翻折到△ABE的位置，试判定四边形AEBC的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：2004年全国中考数学试题汇编《不等式与不等式组》（04）（解析版） 题型：解答题

    （2004•扬州）据电力部门统计，每天8：00至21：00是用电高峰期，简称“峰时”，21：00至次日8：00是用电低谷期，简称“谷时”．为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策．具体见下表：
     时间换表前  换表后
     峰时（8：00-21：00）谷时（21：00-次日8：00）
     电价 0.52元/千瓦时 x元/千瓦时 y元/千瓦时
    已知每千瓦时峰时价比谷时价高0.25元．小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知：峰时用电量占80%，谷时用电量占20%，与换表前相比，电费共下降2元．
    （1）请你求出表格中x和y的值；?
    （2）小卫希望通过调整用电时间，使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元（包括10元和15元）．假设小卫家今后“峰时”用电量占整个家庭用电量的z%，那么，z在什么范围内时，才能达到小卫的期望？

    查看答案和解析>>

    科目：初中数学 来源：2004年全国中考数学试题汇编《二元一次方程组》（02）（解析版） 题型：解答题

    （2004•扬州）据电力部门统计，每天8：00至21：00是用电高峰期，简称“峰时”，21：00至次日8：00是用电低谷期，简称“谷时”．为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策．具体见下表：
     时间换表前  换表后
     峰时（8：00-21：00）谷时（21：00-次日8：00）
     电价 0.52元/千瓦时 x元/千瓦时 y元/千瓦时
    已知每千瓦时峰时价比谷时价高0.25元．小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知：峰时用电量占80%，谷时用电量占20%，与换表前相比，电费共下降2元．
    （1）请你求出表格中x和y的值；?
    （2）小卫希望通过调整用电时间，使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元（包括10元和15元）．假设小卫家今后“峰时”用电量占整个家庭用电量的z%，那么，z在什么范围内时，才能达到小卫的期望？

    查看答案和解析>>

    同步练习册答案