
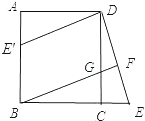
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.

(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
【答案】(1)见解析;(2)四边形E′BGD是平行四边形.
【解析】
试题分析:(1)由正方形ABCD,得BC=CD,∠BCD=∠DCE=90°,又CG=CE,所以△BCG≌△DCE(SAS).
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得四边形E′BGD为平行四边形.
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c﹣3=0的根的情况是( )

A.有两个不相等的实数根
B.有两个异号实数根
C.有两个相等实数根
D.无实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com