练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置，旋转角为a （0°＜a＜90°）．若∠1=110°，则a= ．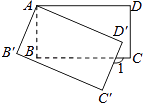

    【答案】20°
    【解析】解：∵矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置，
    ∴∠ADC=∠D=90°，∠DAD′=α，
    ∵∠ABC=90°，
    ∴∠BAD=180°﹣∠2，
    而∠2=∠21=110°，
    ∴∠BAD=180°﹣110°=70°，
    ∴∠DAD′=90°﹣70°=20°，
    即α=20°．
    所以答案是20°．
    【考点精析】掌握旋转的性质是解答本题的根本，需要知道①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道（通道面积不超过总面积的），其余部分铺上草皮．

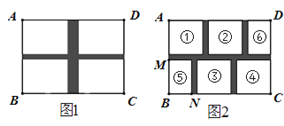
    （1）如图1，若设计两条通道，一条横向，一条纵向，4块草坪为全等的长方形，每块草坪的两边之比为3：4，并且纵向通道的宽度是横向通道宽度的2倍，问横向通道的宽是多少？

    （2）如图2，为设计得更美观，其中草坪①②③④为全等的正方形，草坪⑤⑥为全等的长方形（两边长BN：BM=2：3），通道宽度都相等，问：此时通道的宽度又是多少呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等腰三角形的一条边等于4，另一条边等于9，那么这个三角形的第三边是_______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一家电信公司推出两种移动电话计费方法：计费方法是每月收月租费元，通话时间不超过分钟的部分免费，超过分的按每分钟元加收通话费；计费方法是每月收月租费元，通话时间不超过分钟的部分免费，超过分的按每分钟元加收通话费．设通话时间为分．

    （）用代数式表示通话分钟的通话费用．

    （）用计费方法的用户一个月累计通话分钟所需的话费，若改用计费方法，则可多通话多少分钟？

    （）按， 两种计费方法，所需的话费会相等吗？如果会，请指出相等的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠C＝90°，下列结论正确的是（　　）

    A.sinA＝sinBB.sinA＝cosB

    C.tanA＝tanBD.sinA+sinB＝sinC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)(﹣7)+(﹣5)﹣(﹣13)﹣(+10)

    (2)﹣(﹣1)10×2+(﹣2)3÷4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

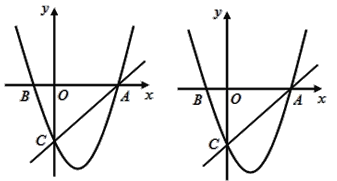
    【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，-3），动点P在抛物线上．

    （1）b =_________，c =_________，点B的坐标为_____________；（直接填写结果）

    （2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

    （3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“a的2倍与b的差不小于0”用不等式表示为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x2-2x+1的值是3，则5-2x2+4x的值是______．

    查看答案和解析>>

    同步练习册答案