
 是关于x的一次函数,且y随x的增大而增大,则m =___ _。
是关于x的一次函数,且y随x的增大而增大,则m =___ _。 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x(度) | 0<x≤140 | | |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.
 沿x轴向右平移2格得线段CD,请你求出线段CD所在的直线函数解析式.
沿x轴向右平移2格得线段CD,请你求出线段CD所在的直线函数解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
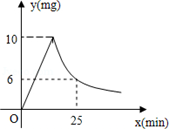
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 进价(元/台) | 售价(元/台) |
| 冰箱 |  | 2500 |
| 彩电 |  | 2000 |
 。
。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | A种产品 | B种产品 |
| 成本 (万元/件) | 0.6 | 0.9 |
| 利润 (万元/件) | 0.2 | 0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com