
【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的面积为______________。
【答案】84或24
【解析】分两种情况考虑:
①当△ABC为锐角三角形时,如图1所示,
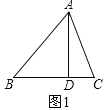
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,AB=15,AD=12,
根据勾股定理得:BD=![]() =9,
=9,
在Rt△ADC中,AC=13,AD=12,
根据勾股定理得:DC=![]() =5,
=5,
∴BC=BD+DC=9+5=14,
则S△ABC=![]() BCAD=84;
BCAD=84;
②当△ABC为钝角三角形时,如图2所示,
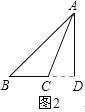
∵AD⊥BC,
∴∠ADB=90°,
在Rt△ABD中,AB=15,AD=12,
根据勾股定理得:BD=![]() =9,
=9,
在Rt△ADC中,AC=13,AD=12,
根据勾股定理得:DC=![]() =5,
=5,
∴BC=BDDC=95=4,
则S△ABC=![]() BCAD=24.
BCAD=24.
综上,△ABC的面积为24或84.
故答案为:24或84.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过![]() .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于![]() .
.

(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 定义:两组邻边分别相等的四边形叫做筝形.
(1)、请写出除定义外的性质和判定猜想各一条,并从定义出发证明你的判定猜想.
(2)、筝型ABCD中,对角线AC,BD相交于点O.
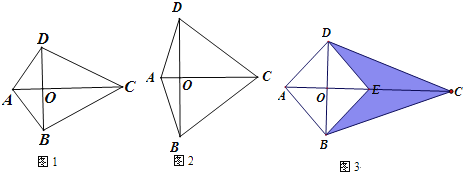
①如图1,若BD=CO,求tan∠BCD的值.
②如图2,若∠DAC=∠BCD=72,求AD:CD的值.
(3)、如图3,把△ABD沿着对角线BD翻折,A点落在对角线AC上的E点.如果△AOD中,一个内角是另一个内角的2倍,且阴影部分图形的面积等于四边形ABED的面积,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO![]() OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
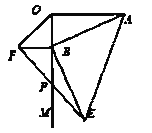
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 几个有理数相乘,当负因数有奇数个时,积为负
B. 几个有理数相乘,当积为负数时,负因数有奇数个
C. 几个有理数相乘,当正因数有奇数个时,积为负
D. 几个有理数相乘,当正因数有奇数个时,和为正
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com