
【题目】如图1,四边形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)填空:![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(2)求![]() 的值;
的值;
(3)将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图2),连接
(如图2),连接![]() ,与
,与![]() 相交于点
相交于点![]() .若
.若![]() ,求
,求![]() 的长.
的长.

【答案】(1)∠BAD+∠ACB=180°;(2)![]() ;(3)1.
;(3)1.
【解析】
试题分析:(1)在△ABD中,根据三角形的内角和定理即可得出结论:∠BAD+∠ACB=180°;
(2)如图1中,作DE∥AB交AC于E.由△OAB≌△OED,可得AB=DE,OA=OE,设AB=DE=CE=CE=x,OA=OE=y,由△EAD∽△ABC,推出![]() ,可得
,可得![]() ,可得4y2+2xy﹣x2=0,即
,可得4y2+2xy﹣x2=0,即![]() ,求出
,求出![]() 的值即可解决问题;
的值即可解决问题;
(3)如图2中,作DE∥AB交AC于E.想办法证明△PA′D∽△PBC,可得![]() ,可得
,可得![]() ,即
,即![]() ,由此即可解决问题;
,由此即可解决问题;
试题解析:(1)如图1中,
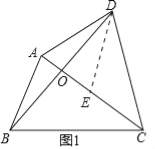
在△ABD中,∵∠BAD+∠ABD+∠ADB=180°,∠ABD+∠ADB=∠ACB,
∴∠BAD+∠ACB=180°,故答案为∠BAD+∠ACB=180°.
(2)如图1中,作DE∥AB交AC于E.
∴∠DEA=∠BAE,∠OBA=∠ODE,
∵OB=OD,∴△OAB≌△OED,
∴AB=DE,OA=OE,设AB=DE=CE=CE=x,OA=OE=y,
∵∠EDA+∠DAB=180°,∠BAD+∠ACB=180°,
∴∠EDA=∠ACB,∵∠DEA=∠CAB,∴△EAD∽△ABC,
∴![]() ,∴
,∴![]() ,
,
∴4y2+2xy﹣x2=0,∴![]() ,
,
∴![]() (负根已经舍弃),∴
(负根已经舍弃),∴![]() .
.
(3)如图2中,作DE∥AB交AC于E.
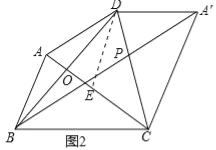
由(1)可知,DE=CE,∠DCA=∠DCA′,∴∠EDC=∠ECD=∠DCA′,
∴DE∥CA′∥AB,∴∠ABC+∠A′CB=180°,
∵△EAD∽△ACB,∴∠DAE=∠ABC=∠DA′C,
∴∠DA′C+∠A′CB=180°,∴A′D∥BC,
∴△PA′D∽△PBC,
∴![]() ,
,
∴![]() ,即
,即![]()
∴PC=1.


科目:初中数学 来源: 题型:
【题目】中国人很早就开始使用负数,曾在一部中国古代数学著作中首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法,这部著作采用按类分章的问题集的形式进行编排,它的出现标志着我国古代数学体系的正式确立.这部经典名著是( )
A.《海岛算经》B.《九章算术》
C.《孙子算经》D.《周髀算经》
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com