【题目】如图，在△ABC中，E，D是BC边的三等分点，F是AC的中点，BF分别交AD，AE于点G，H，则BG∶GH∶HF等于( )
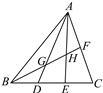
A. 1∶2∶3 B. 3∶5∶2 C. 5∶3∶2 D. 5∶3∶1
【答案】C
【解析】
作FM∥BC交AE于点M，则根据△BEH∽△FMH，利用BF表示出HF的长度，作DN∥AC交BF于点N，则△BDN∽△BCF且△DNG∽△AFG，依据△BDN∽△BCF可以用BF表示出BN的长，然后依据△DNG∽△AFG表示出NG的长，则BG，GM，HF都可以利用BF表示出来，则比值即可求解．
设BC=6a,则BD=DE=EC=2a,作FM∥BC交AE于点M，
∵F是AC的中点，
∴
∵FM∥BC，
∴△BEH∽△FMH，
∴
则
作DN∥AC交BF于点N，设AC=2b，则AF=CF=b，
∴△BDN∽△BCF，
∴
∴
∵DN∥AC，
∴△DNG∽△AFG，
∴
∴
,即
∴
∴
∴
故选：C.
科目：初中数学 来源： 题型：
【题目】如图，直线y=﹣2x+7与x轴、y轴分别相交于点C、B，与直线y=
x相交于点A.
（1）求A点坐标；
（2）如果在y轴上存在一点P，使△OAP是以OA为底边的等腰三角形，则P点坐标是 ；
（3）在直线y=﹣2x+7上是否存在点Q，使△OAQ的面积等于6？若存在，请求出Q点的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
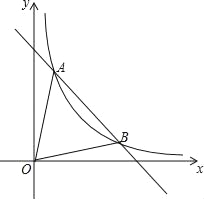
【题目】如图，一次函数y1=﹣x+5的图象与反比例函数y2=
（k≠0）在第一象限的图象交于A（1，n）和B两点．
（1）求反比例函数的解析式；
（2）当y2＞y1＞0时，写出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
，
，
是常数，且
中的
与
的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
|
|
|
|
|
|
|
|
|
|
；
当
时，
；
当
时，的值随值的增大而减小；
方程
有两个不相等的实数根．
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历，我们任意选择其中所示的方框部分，将方框部分中的4个位置的数交叉相乘，再相减，如8×16－9×15=－7,19×27－20×26=－7，不难发现结果都是－7.
（1）请你再选择一组数按上面的方式计算，看看是否符合这个规律.并用你擅长的表达方式描述这个规律.
（2）请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着互联网的发展，互联网消费逐渐深入人们生活，如图是“滴滴顺风车”与“滴滴快车”的行驶里程x（公里）与计费y（元）之间的函数关系图象，下列说法：
（1）“快车”行驶里程不超过5公里计费8元；
（2）“顺风车”行驶里程超过2公里的部分，每公里计费1.2元；
（3）A点的坐标为（6.5，10.4）；
（4）从哈尔滨西站到会展中心的里程是15公里，则“顺风车”要比“快车”少用3.4元，其中正确的个数有（ ）
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF相交于点G.
(1)如图①，若四边形ABCD是矩形，且DE⊥CF.求证：
；
(2)如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；
(3)如图③，若BA＝BC＝9，DA＝DC＝12，∠BAD＝90°，DE⊥CF.求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在国家的宏观调控下，某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
（1）问4、5两月平均每月降价的百分率是多少？
（2）如果房价继续回落，按此降价的百分率，你预测到7月分该市的商品房成交均价是否会跌破3000元/m2？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
