
 已知二次函数过点A(0,-2),B(-1,0),C(
已知二次函数过点A(0,-2),B(-1,0),C(| 5 |
| 4 |
| 9 |
| 8 |
| 1 |
| 2 |
| 5 |
| 4 |
| 9 |
| 8 |
| 1 |
| 2 |
| 5 |
| 4 |
| 9 |
| 8 |
|
| 5 |
| 4 |
| 9 |
| 8 |
|
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
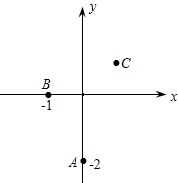 已知二次函数过点A(0,-2),B(-1,0),C(
已知二次函数过点A(0,-2),B(-1,0),C(| 5 |
| 4 |
| 9 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数过点A (0,![]() ),B(
),B(![]() ,0),C(
,0),C(![]() ).
).
(1)求此二次函数的解析式;
(2)判断点M(1,![]() )是否在直线AC上?
)是否在直线AC上?
(3)过点M(1,![]() )作一条直线
)作一条直线![]() 与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
 |
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(33):23.5 二次函数的应用(解析版) 题型:解答题
 )
) )是否在直线AC上;
)是否在直线AC上; )作一条直线l与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
)作一条直线l与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com