
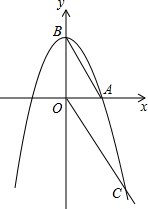
 如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.分析 (1)根据待定系数法即可求得;
(2)根据抛物线解析式求出点A、B的坐标,然后求出∠OBA=45°,再根据∠CPA=∠OBA分点P在点A的左边和右边两种情况求解;
(3)①根据抛物线平移的性质即可求得;②已知了等腰三角形是以OC为底边的等腰三角形,因此Q点必为OC的垂直平分线与抛物线y2的交点,可先求出OC的垂直平分线的解析式,然后联立抛物线的解析式即可求出符合条件的Q点的坐标.
解答 解:(1)∵点C(2,-3)在抛物线y1的图象上,
∴-3=-22+a,解得a=1,
∴抛物线y1的函数表达式y1=-x2+1,
(2)x=0时,y=1,
y=0时,-x2+1=0,解得x1=1,x2=-1,
所以,点A(1,0),B(0,1),
∴∠OBA=45°,
∵点C的坐标为(2,-3),
∵∠CPA=∠OBA,
∴点P在点A的左边时,坐标为(-1,0),
在点A的右边时,坐标为(5,0),
所以,点P的坐标为(-1,0)或(5,0);
(3)①∵点C(2,-3)关于y轴的对称点为(-2,-3),
∴抛物线y1沿x轴向右平移4个单位后得抛物线y2,且抛物线y2的图象过点C,
∴抛物线y2的函数表达式为y=-(x-4)2+1;
②点Q应在线段OC的垂直平分线上,由题意可知,QR⊥OC且平分OC,
∴点P在直线QR上.
∵C(2,-3),
∴OC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,R(1,-$\frac{3}{2}$)
∴OR=$\frac{\sqrt{13}}{2}$,
∵△ORS∽△OEC,
∴$\frac{OS}{OC}$=$\frac{OR}{OE}$,即$\frac{OS}{\sqrt{13}}$=$\frac{\frac{\sqrt{13}}{2}}{3}$,
∴OS=$\frac{13}{6}$,
∴S(0,-$\frac{13}{6}$)
∴直线QR的解析式为y=$\frac{2}{3}$x-$\frac{13}{6}$,
又点Q是直线y=$\frac{2}{3}$x-$\frac{13}{6}$与抛物线y=-(x-4)2+1的交点,
故可得$\left\{\begin{array}{l}{y=-(x-4)^{2}+1}\\{y=\frac{2}{3}x-\frac{13}{6}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{22+\sqrt{22}}{6}}\\{{y}_{1}=\frac{5+2\sqrt{22}}{18}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{22-\sqrt{22}}{6}}\\{{y}_{2}=\frac{5-2\sqrt{22}}{18}}\end{array}\right.$;
故符合条件的点Q的横坐标为$\frac{22+\sqrt{22}}{6}$或$\frac{22-\sqrt{22}}{6}$.
点评 本题着重考查了待定系数法求一次函数和二次函数解析式、图形平移变换、等腰三角形的判定,相似三角形的判定和性质等重要知识点,求得二次函数的解析式以及平移后的解析式是本题的关键,(3)通过三角形相似求得S的坐标进而求得解析式是本题的难点.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
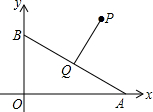 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
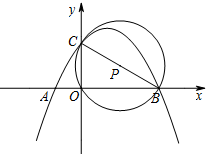 如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.
如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.
如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
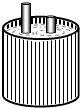 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1>b-1 | B. | 2a>2b | C. | $\frac{a}{3}$$>\frac{b}{3}$ | D. | -4a>-4b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com