
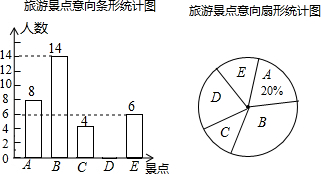
分析 (1)用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数;
(2)先计算出最想去D景点的人数,再补全条形统计图,然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)用800乘以样本中最想去A景点的人数所占的百分比即可.
解答 解:(1)被调查的学生总人数为8÷20%=40(人);
(2)最想去D景点的人数为40-8-14-4-6=8(人),
补全条形统计图为:
扇形统计图中表示“最想去景点D”的扇形圆心角的度数为$\frac{8}{40}$×360°=72°;
(3)800×$\frac{14}{40}$=280,
所以估计“最想去景点B“的学生人数为280人.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.从条形图可以很容易看出数据的大小,便于比较.也考查了扇形统计图和利用样本估计总体.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,已知∠AOB=40°,现按照以下步骤作图:
如图所示,已知∠AOB=40°,现按照以下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
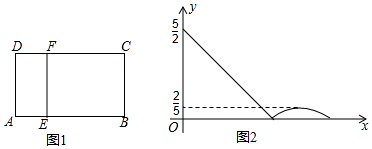
| A. | $\frac{23}{5}$ | B. | 5 | C. | 6 | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
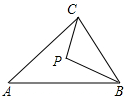 如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )| A. | 110° | B. | 125° | C. | 130° | D. | 65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com