
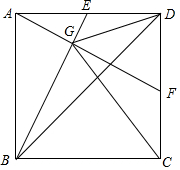
 正方形ABCD中,E、F分别是AD、DC的中点,BE和AF交于点G,∠DGF=∠DBC,求证:GC=BC.
正方形ABCD中,E、F分别是AD、DC的中点,BE和AF交于点G,∠DGF=∠DBC,求证:GC=BC. 分析 如图,延长AF交BC的延长线于M,△BAE≌△ADF,推出∠BGM=90°,由△ADF≌△MCF,推出AD=CM=BC,再根据直角三角形斜边中线性质即可证明.
解答 证明:如图,延长AF交BC的延长线于M.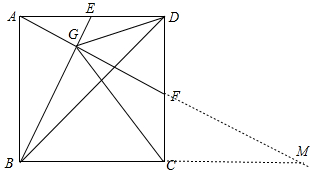
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAC=∠ADC=∠BCD=∠DCM=90°,
∵AE=ED,DF=FC,
∴AE=DF,
在ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠ADF}\\{AE=DF}\end{array}\right.$,
∴△BAE≌△ADF,
∴∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AGE=∠BGM=90°,
在△ADF和△MCF中,
$\left\{\begin{array}{l}{∠ADF=∠MCF=90°}\\{DF=FC}\\{∠AFD=∠MFC}\end{array}\right.$,
∴△ADF≌△MCF,
∴AD=CM=BC,
在Rt△BGM中,∵BC=CM,
∴CG=CB=CM,
∴GC=BC.
点评 本题考查正方形的性质、全等三角形的判定和性质,直角三角形斜边中线的性质等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题,注意AF与BE垂直这个结论的应用和证明,属于中考常考题型.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:解答题
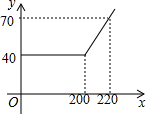 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com