
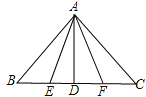
【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
【答案】4.
【解析】试题分析:本题重点是根据已知条件“AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点”,得出△ABD≌△ACD,然后再由结论推出AB=AC,BE=DE,CF=DF,从而根据“SSS”或“SAS”找到更多的全等三角形,要由易到难,不重不漏.
解:∵AD⊥BC,AB=AC
∴D是BC中点
∴BD=DC,
∵AD=AD,
∴△ABD≌△ACD(SSS);
E、F分别是DB、DC的中点
∴BE=ED=DF=FC
∵AD⊥BC,AD=AD,ED=DF
∴△ADF≌△ADE(HL);
∵∠B=∠C,BE=FC,AB=AC
∴△ABE≌△ACF(SAS)
∵EC=BF,AB=AC,AE=AF
∴△ABF≌△ACE(SSS).
∴全等三角形共4对,分别是:△ABD≌△ACD(HL),△ABE≌△ACF(SAS),△ADF≌△ADE(SSS),△ABF≌△ACE(SAS).
故答案为4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成“ ”形状,折叠过程按图
”形状,折叠过程按图![]() 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长![]() 厘米,分别回答下列问题:
厘米,分别回答下列问题:
(1)如图①、图②,如果长方形纸条的宽为![]() 厘米,并且开始折叠时
厘米,并且开始折叠时![]() 厘米,那么在图②中,
厘米,那么在图②中,![]() ____厘米.
____厘米.
(2)如图②,如果长方形纸条的宽为![]() 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形,![]() ______厘米.
______厘米.
(3)如图④,如果长方形纸条的宽为![]() 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点![]() 与点
与点![]() 的距离(结果用
的距离(结果用![]() 表示) .
表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
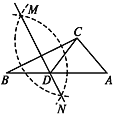
A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
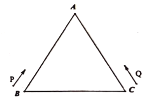
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com