
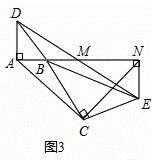
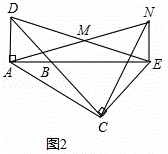
��ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
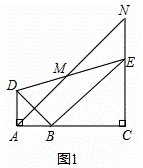
��1����A��B��C������ͬһֱ����ʱ����ͼ1 ������֤��MΪAN���е㣻
������֤��MΪAN���е㣻
��2����ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2������֤����ACNΪ����ֱ�������Σ�
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3λ��ʱ����2���еĽ����Ƿ��Գ���������������֤��֮��������������˵�����ɣ�

��1��֤������ͼ1��
��EN��AD��
���MAD=��MNE����ADM=��NEM��
�ߵ�MΪDE���е㣬
��DM=EM��
�ڡ�ADM�͡�NEM�У�
��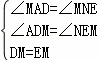 ��
��
���ADM�ա�NEM��
��AM=MN��
��MΪAN���е㣮
��2��֤������ͼ2��
�ߡ�BAD�͡�BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45�㣮
��AD��NE��
���DAE+��NEA=180�㣮
�ߡ�DAE =90�㣬
=90�㣬
���NEA=90�㣮
���NEC=135�㣮
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135�㣮
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
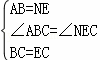
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ�������Σ�
��3����ACN��Ϊ����ֱ�������Σ�
֤������ͼ3����ʱA��B��N������ͬһ��ֱ���ϣ�
��AD��EN����DAB=90�㣬
���ENA=��DAN=90�㣮
�ߡ�BCE=90�㣬
���CBN+��CEN=360�㩁90�㩁90��=180�㣮
��A��B��N������ͬһ��ֱ���ϣ�
���ABC+��CBN=180�㣮
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
 �ڡ�ABC�͡�NEC�У�
�ڡ�ABC�͡�NEC�У�
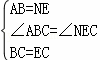
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������ABC�����߳��ֱ�Ϊ2��3���������ABC���ܳ�Ϊ��������
| �� | A�� | 7 | B�� | 8 | C�� | 6��8 | D�� | 7��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
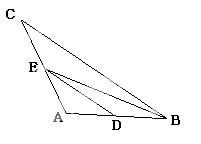
��ͼ��BE�ǡ�ABC�Ľ�ƽ���ߣ�DE��BC����AB�ڵ�D����A=126�㣬
��DEB=14�㣬���BEC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵxOy�У�������ABCD�Ķ���A��B������ֱ�Ϊ����3��0������2��0������D��y���ϣ����C��������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
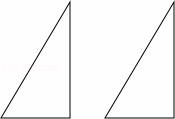
��ͼ������ȫ�ȵĺ�30��ǵ�ֱ�������Σ�
��1��������ȱ�ƴ��һ�����һ��û���ص����ֵ�ƽ��ͼ�Σ����㻭�����в�ͬ��ƴ��ƽ��ͼ�ε�ʾ��ͼ��
��2��������1����ƽ��ͼ�ηֱ�ӡ�����ʵء���״����С��ȫ��ͬ�Ŀ�Ƭ�ϣ�ϴ�Ⱥ���������ȡһ�ţ����ȡ�Ŀ�Ƭ��ƽ��ͼ��Ϊ��Գ�ͼ�εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2014��5�³����н����־��еġ�����ʫ���С��ݽ������У���11��ѧ���μӾ��������Ǿ����ijɼ�������ͬ�����е�һ��ѧ����֪���Լ��ܷ����ǰ6��������Ҫ�˽��Լ��ijɼ�����Ҫ�˽���11��ѧ���ɼ��ģ�������
| �� | A�� | ���� | B�� | ��λ�� | C�� | ƽ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�����������ó߹�����AOB�Ľ�ƽ����OC�����������ó߹�����ƽ���߹����У��õ���������ȫ�ȵ��ж����� �ǣ�������
�ǣ�������
������
����OΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�OA��OB�ڵ�D��E��
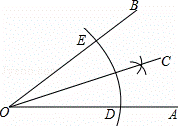
�ڷֱ���D��EΪԲ�ģ����� DE�ij�Ϊ�뾶�����������ڡ�AOB�ڽ���һ��C��
DE�ij�Ϊ�뾶�����������ڡ�AOB�ڽ���һ��C��
�ۻ�����OC������OC���ǡ�AOB�Ľ�ƽ���ߣ�
| �� | A�� | ASA | B�� | SAS | C�� | SSS | D�� | AAS |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com