
分析 (1)设比值为k(k≠0),用k表示出a、b、c,然后代入比例式进行计算即可得解;
(2)将sin30°=$\frac{1}{2}$,tan45°=1,cos60°=$\frac{1}{2}$代入进行计算即可得解.
解答 解:(1)设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{5}$=k(k≠0),
则a=2k,b=3k,c=5k,
所以,$\frac{3a+4b}{5b-c}$=$\frac{3•2k+4•3k}{5•3k-5k}$=$\frac{9}{5}$;
(2)2sin30°-tan45°+$\sqrt{3}$cos60°,
=2×$\frac{1}{2}$-1+$\sqrt{3}$×$\frac{1}{2}$,
=1-1+$\frac{\sqrt{3}}{2}$,
=$\frac{\sqrt{3}}{2}$.
点评 本题考查了比例式的性质,特殊角的三角函数值,(1)用k表示出a、b、c求解更简便,(2)熟记特殊角的三角函数值是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 有公共顶点的两个角是对顶角 | B. | 在一条直线上任取一点A | ||
| C. | 过点A作直线MN的垂线 | D. | 过点A作直线MN的平行线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-3})}^2}}=3$ | B. | $\sqrt{3}×\sqrt{2}=\sqrt{6}$ | C. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | D. | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=2x2-m的顶点为P,与x轴交于点A,B,且△ABP是等腰直角三角形,则m的值是( )
如图,抛物线y=2x2-m的顶点为P,与x轴交于点A,B,且△ABP是等腰直角三角形,则m的值是( )| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 平均数 | 众数 | 中位数 | 方差 |
| 9.15 | 9.2 | 9.1 | 0.2 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一棵树在一次强台风中,从离地面3米折断,量得倒下部分树尖与树根的距离是4米,这棵树在折断前的高度是( )
如图,一棵树在一次强台风中,从离地面3米折断,量得倒下部分树尖与树根的距离是4米,这棵树在折断前的高度是( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
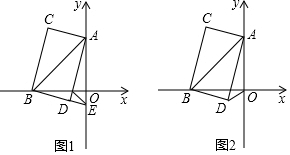
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com