
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①abc>0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.其中正确的结论有( )个.
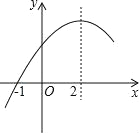
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
①根据抛物线开口方向和与y轴的交点,则a<0,c>0,由对称轴为直线x=![]() =2,则有b=﹣4a>0,于是abc<0;
=2,则有b=﹣4a>0,于是abc<0;
②观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;
③由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;
④由于对称轴为直线x=2,根据二次函数的性质得到当﹣1<x<2时,y的值随x值的增大而增大.
①∵抛物线开口向下,∴a<0.
∵抛物线交y轴的正半轴,∴c>0.
∵抛物线的对称轴为直线x=![]() =2,∴b=﹣4a>0,∴abc<0,故本结论错误;
=2,∴b=﹣4a>0,∴abc<0,故本结论错误;
②∵当x=﹣3时,y<0,∴9a﹣3b+c<0,即9a+c<3b,故本结论错误;
③∵抛物线与x轴的一个交点为(﹣1,0),∴a﹣b+c=0,而b=﹣4a,∴a+4a+c=0,即c=﹣5a,∴8a+7b+2c=8a﹣28a﹣10a=﹣30a.
∵抛物线开口向下,∴a<0,∴8a+7b+2c>0,故本结论正确;
④∵对称轴为直线x=2,∴当﹣1<x<2时,y的值随x值的增大而增大,当x>2时,y随x的增大而减小,故本结论错误.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一圆内接正八边形ABCDEFGH,若△ADE的面积为8,则正八边形ABCDEFGH的面积为( )
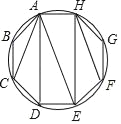
A. 32 B. 40 C. 24 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字1,2,3;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,﹣3,现从甲袋中随机摸出一个小球,将标有的数字记录为x,再从乙袋中随机摸出一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
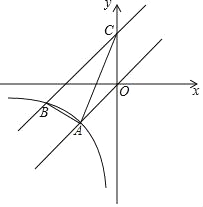
【题目】已知:如图,在平面直角坐标系中,正比例函数y=x的图象与反比例函数y=![]() (k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(1)求该反比例函数的解析式与平移后的直线解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两个全等的等腰直角三角形ABC和EDC中,∠ACB=∠ECD=90°,点A与点E重合,点D与点B重合.现△ABC不动,把△EDC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°).
(1)如图②,AB与CE交于点F,ED与AB,BC分别交于点M,H.求证:CF=CH;
(2)如图③,当α=45°时,试判断四边形ACDM的形状,并说明理由;
(3)如图②,在△EDC绕点C旋转的过程中,连结BD,当旋转角α的度数为多少时,△BDH是等腰三角形?



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )

(A).(4.8,6.4) (B).(4,6) (C)(5.4,5.8) (D).(5,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
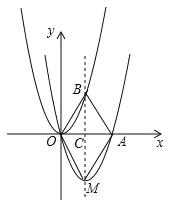
【题目】如图,在平面直角坐标系中,抛物线y1=ax(x﹣2)与x轴交于O、A两点,顶点为M,对称轴BM交抛物线![]() 于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
特例探究:填表:

归纳证明:
当a=2时,证明四边形OMAB是菱形;
拓展应用
(1)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,当四边形OMAB为正方形时,a= ,m= .
(2)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,S= (用含m的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com