
 如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$.
如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$. 分析 连接CE,AE,过C作CM⊥AB于M,根据菱形的性质得到AE=2$\sqrt{3}$,∠EA=30°,解直角三角形得到AB=4$\sqrt{3}$,AM=2$\sqrt{3}$=AE,根据全等三角形的性质得到CE=CM=6,∠ECA=∠MCA=30°,得到∠ECB=90°,得到CG=$\frac{1}{2}$BE=$\frac{1}{2}$×$\sqrt{C{E}^{2}+C{B}^{2}}$=$\frac{1}{2}$×2$\sqrt{21}$=$\sqrt{21}$,过G作GH⊥CE于H,交AC于N,根据三角形的中位线的性质得到CH=3,GH=$\frac{1}{2}$BC=$\frac{1}{2}×$4$\sqrt{3}$=2$\sqrt{3}$,根据全等三角形的性质得到DN=DE=2,∠AND=∠AED=30°,由勾股定理即可得到结论.
解答 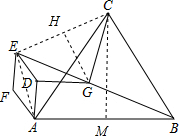 解:连接CE,AE,过C作CM⊥AB于M,
解:连接CE,AE,过C作CM⊥AB于M,
在菱形ADEF中,∵AD=2,∠DAF=60°,
∴AE=2$\sqrt{3}$,∠EA=30°,
∵AD⊥AB,∠CAB=60°,
∴∠DAC=30°,
∴∠EAC=60°,
在等边三角形ACB中,AB=4$\sqrt{3}$,
∴AM=2$\sqrt{3}$=AE,
在△AEC与△AMC中,$\left\{\begin{array}{l}{AE=AM}\\{∠EAC=∠MAC=60°}\\{AC=AC}\end{array}\right.$,
∴△AEC≌△AMC,
∴CE=CM=6,∠ECA=∠MCA=30°,
∴∠ECB=90°,
∵点G为线段BE的中点,
∴CG=$\frac{1}{2}$BE=$\frac{1}{2}$×$\sqrt{C{E}^{2}+C{B}^{2}}$=$\frac{1}{2}$×2$\sqrt{21}$=$\sqrt{21}$,
过G作GH⊥CE于H,交AC于N,
∴GH∥BC,
∵点G为线段BE的中点,
∴H为CE的中点,
∴CH=3,GH=$\frac{1}{2}$BC=$\frac{1}{2}×$4$\sqrt{3}$=2$\sqrt{3}$,
∵∠NCH=30°,
∴NH=$\sqrt{3}$,CN=2$\sqrt{3}$,
∵AC=4$\sqrt{3}$,
∴AN=2$\sqrt{3}$,
∴AE=2$\sqrt{3}$=AN,
在△DAE与△DAN中,$\left\{\begin{array}{l}{AE=AN}\\{∠EAD=∠DAN}\\{AD=AD}\end{array}\right.$,
∴△DAE≌△DAN,
∴DN=DE=2,∠AND=∠AED=30°,
∵∠ANG=60°,
∴∠DNG=90°,
∴DG=$\sqrt{D{N}^{2}+N{G}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$,$\sqrt{21}$.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,勾股定理,三角形中位线的性质,正确的作出辅助线是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 79.5×105 | B. | 7.95×106 | C. | 7.95×102 | D. | 0.795×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 过⊙O上任意一点B作过圆心O的直线交⊙O于另一点E,点A为BE延长线上任意一点,过点A作⊙O的切线AB,切点为点D,过B作BC⊥AD于C,BC交⊙O于点F,连BD
过⊙O上任意一点B作过圆心O的直线交⊙O于另一点E,点A为BE延长线上任意一点,过点A作⊙O的切线AB,切点为点D,过B作BC⊥AD于C,BC交⊙O于点F,连BD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com