
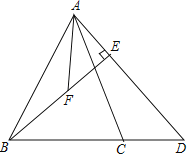
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
【答案】(1)![]() ;(2)9;(3)见详解
;(2)9;(3)见详解
【解析】
(1)在Rt△AEB中,利用勾股定理即可解决问题;
(2)由∠D=45°可证得BE=DE,再利用三角的面积公式计算即可;
(3)如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MFB,再证明△ABM≌△ACD即可.
(1)解:∵AB=AC,AC=![]() ,
,
∴AB=![]() ,
,
∵BE⊥AD,AE=![]() ,
,
∴在Rt△AEB中,![]() ;
;
(2)解:∵BE⊥AD,∠D=45°,
∴∠EBD=∠D =45°,
∴BE=DE=![]() ,
,
∴AD=AE+DE=![]() ,
,
∴![]() ;
;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
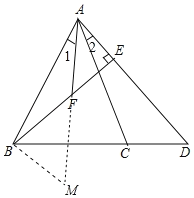
∵点F为BE的中点,
∴EF=BF,
在△AEF和△MBF中,
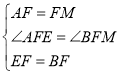
∴△AEF≌△MBF(SAS),
∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.
又∵∠BAC=∠DAF,
∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,
∴∠1=∠2.
在△ABM和△ACD中,
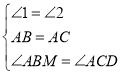 ,
,
∴△ABM≌△ACD(ASA),
∴AM=AD,
又∵AM=AF+MF=2AF,
∴2AF=AD.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
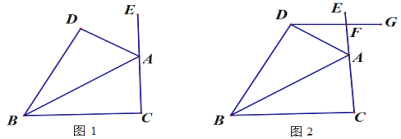
【题目】已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.
(1)若AC⊥BC,求∠BAE的度数;
(2)请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大叔销售牛肉干,已知甲客户购买了12包五香味的和10包原味的共花了146元,乙客户购买了6包五香味的和8包原味的共花了88元.
(1)现在老师带了200元,能否买到10包五香味牛肉干和20包原味牛肉干?
(2)现在老师想刚好用完这200元钱,你能想出哪些牛肉干的包数组合形式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
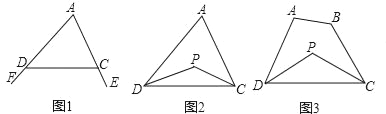
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在平面直角坐标系中,已知抛物线![]() +n过点A(4,0),B (1,-3).
+n过点A(4,0),B (1,-3).

(1)求抛物线的表达式及顶点D的坐标;
(2)将![]() 时函数的图象记为G,点P为G上一动点,求P点纵坐标
时函数的图象记为G,点P为G上一动点,求P点纵坐标![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若经过点C(4,-4)的直线![]() 与图象G有两个公共点,结合图象直接写出b的取值范围.
与图象G有两个公共点,结合图象直接写出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com