
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ ![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2. 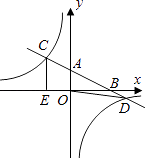
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+6与x轴、y轴分别交于点A、B两点,与正比例函数y=k2x交于点D(2,2)
(1)求一次函数和正比例函数的表达式;
(2)若点P(m,m)为直线y=k2x上的一个动点(点P不与点D重合),点Q在一次函数y=k1x+6的图象上,PQ∥y轴,当PQ=![]() OA时,求m的值.
OA时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC= ![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( ) 
A.![]()
B.![]()
C.![]() +1
+1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com