
 ),点C的坐标为(
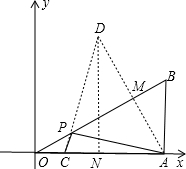
),点C的坐标为(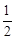 ,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).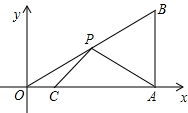
A.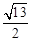 | B.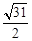 |
C.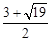 | D.2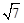 |
 ),∴AB=
),∴AB= ,OA=3,∠B=60°.
,OA=3,∠B=60°. .
.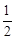 ×OA×AB=
×OA×AB=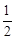 ×OB×AM,∴AM=
×OB×AM,∴AM=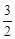 .∴AD=2×
.∴AD=2×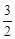 =3.
=3.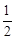 AD=
AD=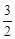 .
.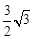 .
.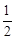 ,0),∴
,0),∴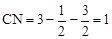 .
.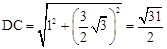 .
.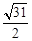 .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:不详 题型:解答题

 轴对称,并写出B1的坐标;(4分)
轴对称,并写出B1的坐标;(4分)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(0,672 ) | B.(672,0) | C.(44,10) | D.(10,44) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
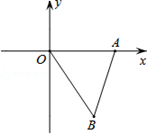
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
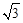 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为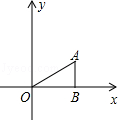
A.(﹣1,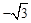 ) ) | B.(﹣1,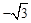 )或(﹣2,0) )或(﹣2,0) | C.(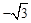 ,﹣1)或(0,﹣2) ,﹣1)或(0,﹣2) | D.(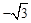 ,﹣1) ,﹣1) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
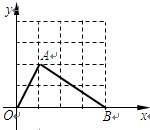
| A.(-3,2) | B.(5,2) | C.(-4,2) | D.(3,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com