
 д�������������֪����֤�������֤�����̣�
д�������������֪����֤�������֤�����̣����� ��ƽ���ı��ε����ʵó���BAC=��DCA�����ɽ�ƽ����֤����BAC=��BCA���ɵȽǶԵȱߵó�AB=CB�����ɵó����ۣ�
��� ��֪���ı���ABCD��ƽ���ı��Σ��Խ���ACƽ�֡�BCD��
��֤��ƽ���ı���ABCD�����Σ�
֤�������ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���BAC=��DCA��
��ACƽ�֡�BCD��
���BCA=��DCA��
���BAC=��BCA��
��AB=CB��
��ƽ���ı���ABCD�����Σ�
�ʴ�Ϊ���ı���ABCD��ƽ���ı��Σ��Խ���ACƽ�֡�BCD��
ƽ���ı���ABCD�����Σ�
���ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���BAC=��DCA��
��ACƽ�֡�BCD��
���BCA=��DCA��
���BAC=��BCA��
��AB=CB��
��ƽ���ı���ABCD�����Σ�
���� ���⿼�������ε��ж�������ƽ���ı��ε����ʣ���������ƽ���ı��ε����ʣ����ܽ���������֤�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
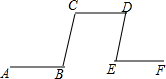 ��ͼ��AB��CD��EF��BC��DE�����B���E�Ĺ�ϵ�ǣ�������
��ͼ��AB��CD��EF��BC��DE�����B���E�Ĺ�ϵ�ǣ�������| A�� | ��� | B�� | ���� | C�� | ���� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AE�ǵȱ�������ABC��BC�ϵĸߣ�AB=4��DC��BC������ΪC��CD=$\sqrt{3}$��BD��AE��AC�ֱ��ڵ�F��M��
��ͼ��AE�ǵȱ�������ABC��BC�ϵĸߣ�AB=4��DC��BC������ΪC��CD=$\sqrt{3}$��BD��AE��AC�ֱ��ڵ�F��M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com