

分析 (1)①根据题意直接画出图形得出即可;
②利用对称的性质以及等角对等边的性质,进而得出答案;
(2)利用对称的性质以及等角对等边进而得出答案;
(3)由轴对称的性质可得:,进而利用勾股定理得出答案.
解答 解:(1)①如图1所示:
②如图2,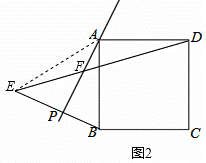
连接AE,由对称得,
∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADF=$\frac{180°-130°}{2}$=25°;
(2)如图2,
连接AE,由对称得
∠PAB=∠PAE=α,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=α,
∴∠EAD=90°+2α,
∴∠ADF=$\frac{180°-(90°+2α)}{2}$=45°-α.
(3)如图3,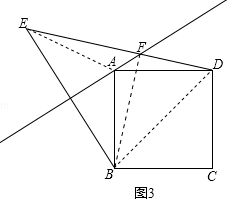
连接AE、BF、BD,
由对称可知,EF=BF,AE=AB=AD,
∠ABF=∠AEF=∠ADF,
∴∠BFD=∠BAD=90°,
在Rt△BDF中,BF2+FD2=BD2,
在Rt△ABC中,BD=$\sqrt{2}$AB,
∴EF2+FD2=2AB2.
点评 此题是四边形综合题,主要考查了正方形的性质以及勾股定理和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.


科目:初中数学 来源: 题型:选择题
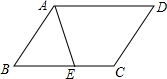 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 为了了解“嫦娥二号”卫星零部件的状况 | |
| C. | 学校招聘教师,对应聘人员面试 | |
| D. | 了解一批灯泡的使用寿命 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com