
【题目】已知二次函数y=x2+bx+c的图象经过(0,3),(4,3).
(1)求b、c的值.
(2)开口方向 ,对称轴为 ,顶点坐标为 .
(3)该函数的图象怎样由y=x2的图象平移得到.
【答案】(1)b=-4,c=3;(2)向上,直线x=2,(2,﹣1);(3)y=(x﹣2)2﹣1是由y=x2向右平移2个单位,向下平移1个单位得到的.
【解析】
(1)将(0,3)(4,3)两点坐标代入y=x2+bx+c,解方程即可求得b、c的值;
(2)根据二次函数的性质,利用配方法求出求出函数的最值与对称轴即可;
(3)根据平移规律直接回答即可.
解:(1)由于二次函数y=x2+bx+c的图象经过点(0,3)、(4,3),
则![]() ,解得:
,解得:![]() ;
;
(2)由二次函数y=x2﹣4x+3可知:a=1,开口方向向下;
原二次函数经变形得:y=(x﹣2)2﹣1,
故顶点为(2,﹣1),对称轴是直线x=2
故答案为向上,直线x=2,(2,﹣1);
(3)y=(x﹣2)2﹣1是由y=x2向右平移2个单位,向下平移1个单位得到的.


科目:初中数学 来源: 题型:
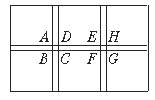
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示
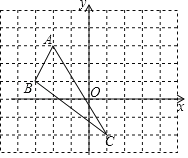
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小垣用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | ______ | … | ______ |
(2)根据小垣的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.

![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com