
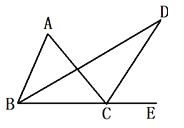
【题目】在ΔABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.
(2)由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.
【答案】答案见解析
【解析】试题分析:(1)根据三角形内角和定理和角平分线的性质,已知∠ABC=60°,∠ACB=40°,易求∠A和∠D度数.(2)根据三角形外角的性质以及角平分线性质,可得∠ACE=2∠D+∠ABC,∠ACE=∠A+∠ABC,即可得∠A和∠D的数量关系.
试题解析:解:(1)∵∠ABC=60°,∠ACB=40°,∴∠A=80°.
∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=30°.
又∵∠ACB=40°,
∴∠ACE=140°.
又∵CD是∠ACE的平分线,
∴∠DCE=70°.
∴∠D=40°
(2)∠A=2∠D.
证明:∵CD 平分∠ACE
∴∠ACE=2∠DCE
又∠DCE=∠D+∠DBC
∴2∠DCE=2∠D+2∠DBC
∵BD平分∠ABC
∴∠ABC=2∠DBC
即∠ACE=2∠D+∠ABC
而∠ACE=∠A+∠ABC
∴2∠D=∠A


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a.
如:1⊕3=1×32+2×1×3+1=16.
(1)求(﹣2)⊕3的值;
(2)若(a⊕3)⊕1=128,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会的主题馆与中国馆利用太阳能发电,年发电量可达2 840 000度.2 840 000用科学记数法可表示为 . (保留两个有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐老师给爱好学习的小敏和小捷提出这样一个问题:如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
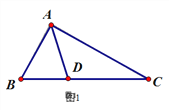
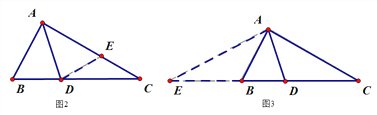
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)请你任意选择一种思路继续完成下一步的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使![]() ?若存在请求出点P坐标,若不存在请说明理由.
?若存在请求出点P坐标,若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB的平分线相交于点D,求∠BDC的度数.
(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快4G网络建设,某市电信运营企业根据自身发展规划,2014年计划完成投资28000000元,将28000000用科学记数法可表示为( )
A. 2.8×104B. 0.28×108C. 2.8×107D. 28×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com