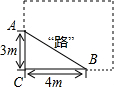
如图.某学校有一块长方形花圃.有极少数人为了避开拐角走“捷径 .在花圃内走出了一条“路 AB.爱心小组想在A处树立一个标牌“少走■米.踏之何刃? 请你计算后帮她们在标牌的■填上适当的数字为2米．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

20．

如图，某学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”AB，爱心小组想在A处树立一个标牌“少走■米，踏之何刃？”请你计算后帮她们在标牌的■填上适当的数字为2米．

分析利用勾股定理求出AB的长即可解决问题．

解答解：在Rt△ABC中，∵AC=3m，BC=4m，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5m，
3+4-5=2，
故答案为2米．

点评本题考查勾股定理的应用，解题的关键是理解题意，灵活运用勾股定理解决实际问题，属于中考常考题型．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

10．已知点A（a-1，5）和点B（2，b-1）关于x轴成轴对称，则（a+b）²⁰¹⁶=1．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

11．

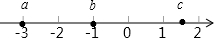已知有理数a，b，c在数轴上的位置如图所示，则下列说法中不正确的是（　　）

	A．	a=-3		B．	b=-1
	C．	a的相反数大于b的相反数		D．	c可能等于2.5

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

有理数m，n在数轴上的位置如图所示，化简$\sqrt{{m}^{2}}$-$\sqrt{{n}^{2}}$-$\sqrt{（m-n）^{2}}$=-2n．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．若14x⁶y²与-31x^3my²的和是单项式，则式子12m-24的值是（　　）

A．

-3

B．

-5

C．

-4

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．阅读下列解题过程：$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{1×（\sqrt{5}-\sqrt{4}）}{（\sqrt{5}+\sqrt{4}）（\sqrt{5}-\sqrt{4}）}$=$\frac{\sqrt{5}-\sqrt{4}}{（\sqrt{5}）^{2}-（\sqrt{4}）^{2}}$=$\sqrt{5}$-$\sqrt{4}$=$\sqrt{5}$-2；
$\frac{2}{\sqrt{6}-\sqrt{5}}$=$\frac{2×（\sqrt{6}+\sqrt{5}）}{（\sqrt{6}-\sqrt{5}）（\sqrt{6}+\sqrt{5}）}$=$\frac{2\sqrt{6}+2\sqrt{5}}{（\sqrt{6}）^{2}-（\sqrt{5}）^{2}}$=2$\sqrt{6}$+2$\sqrt{5}$；
请解答下列问题：
（1）观察上面解题过程，计算$\frac{3}{\sqrt{10}-\sqrt{7}}$；
（2）请直接写出$\frac{1}{\sqrt{n}+\sqrt{n-1}}$的结果．（n≥1）
（3）利用上面的解法，请化简：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{98}+\sqrt{99}}$+$\frac{1}{\sqrt{99}+\sqrt{100}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，求∠CDF的度数．