对于-元二次方程ax2+bx+c=O(a≠0),下列说法:
①当b=0时,方程ax2+bx+c=O一定有两个互为相反数的实数根;
②当b≠0且c=0时,方程ax2+bx+c=O一定有两个实数根且有一根为0;
③当a+b+c=0时,方程ax2+bx+c=O一定有两个不相等的实数根;
④当a>0,c>0且a-b+c<0时,方程ax2+bx+c=O一定有两个不相等的实数根.
其中正确的是( )
A.①②③
B.①②④
C.②③④
D.②④、
【答案】
分析:将①②③④的条件分别应用到ax
2+bx+c=O,根据不同的解析式,利用根与系数的关系解答即可.
解答:解:①当b=0时,方程ax
2+bx+c=O化为ax
2+c=O,当c<0时,方程无解,故方程不一定有两个互为相反数的实数根;
②当b≠0且c=0时,方程ax
2+bx+c=O化为ax
2+bx=O,解得x=0或x=-
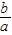
,可知方程一定有两个实数根且有一根为0;
③当a+b+c=0时,方程ax
2+bx+c=O中,△=b
2-4ac=(a+c)
2-4ac=(a-c)
2≥0,故方程不一定有两个不相等的实数根;
④当a>0,c>0且a-b+c<0时,方程ax
2+bx+c=O的解可认为是y=ax
2+bx+c与x轴的交点横坐标,
∵a>0,故函数开口向上,
∵a-b+c<0,
可知x=-1时,
函数值<0,
故y=ax
2+bx+c与x轴有两个交点.
∴方程ax
2+bx+c=O一定有两个不相等的实数根.
故选D.
点评:此题考查了一元二次方程根的判别式,方程变形后,分别利用一元二次方程根的判别式进行解答即可.而对于④,要利用二次函数与一元二次方程的关系解答.

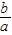 ,可知方程一定有两个实数根且有一根为0;
,可知方程一定有两个实数根且有一根为0;

 名校课堂系列答案
名校课堂系列答案