
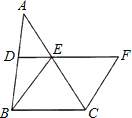
【题目】如图所示,在△![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形BCEF是菱形;
(2)若![]() ,
,![]() ,求菱形BCEF的面积.
,求菱形BCEF的面积.
【答案】(1)见解析;(2)18![]()
【解析】
(1)由D、E分别是AB、AC的中点,BE=2DE,易证得EF=BC,EF∥BC,即可判定四边形BCFE是平行四边形,又由EF=BE,即可证得四边形BCFE是菱形;
(2)由∠BCF=120°,易证得△EBC是等边三角形,又由CE=6,即可求得菱形BCFE的高,继而求得菱形BCFE的面积.
解:(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)解:∵∠BEF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BE=BC=CE=6,
过点E作EG⊥BC于点G,
∴EG=BEsin60°=6×![]() =3
=3![]() ,
,
∴S菱形BCFE=BCEG=6×3![]() =18
=18![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
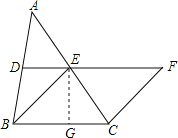
【题目】将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合,DF=8.
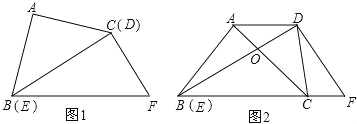
(1)若P是BC上的一个动点,当PA=DF时,求此时∠PAB的度数;
(2)将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
①探求△CDO的形状,并说明理由;
②在图①中,若P是BC的中点,连接FP,将等腰直角三角板ABC绕点B顺时针旋转,当旋转角α= 时,FP长度最大,最大值为 (直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向右平移2个单位,得到新的函数图象
的图象向右平移2个单位,得到新的函数图象![]() .
.
①直接写出函数图象![]() 的表达式;
的表达式;
②设直线![]() 与
与![]() 轴交于点A,与y轴交于点B,当线段AB与图象
轴交于点A,与y轴交于点B,当线段AB与图象![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
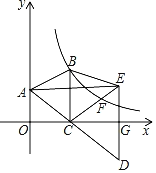
【题目】如图,在△ABC中,AB=AC,点A在y轴上,点C在x轴上,BC⊥x轴,tan∠ACO=![]() .延长AC到点D,过点D作DE⊥x轴于点G,且DG=GE,连接CE,反比例函数y=
.延长AC到点D,过点D作DE⊥x轴于点G,且DG=GE,连接CE,反比例函数y=![]() (k≠0)的图象经过点B,和CE交于点F,且CF:FE=2:1.若△ABE面积为6,则点D的坐标为_____.
(k≠0)的图象经过点B,和CE交于点F,且CF:FE=2:1.若△ABE面积为6,则点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
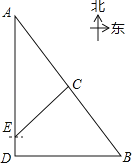
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
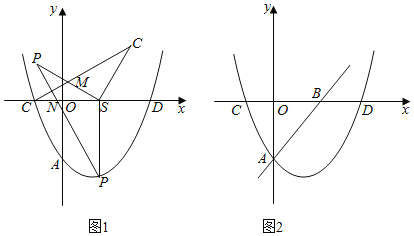
【题目】如图1,抛物线y=a(x+2)(x﹣6)(a>0)与x轴交于C,D两点(点C在点D的左边),与y轴负半轴交于点A.
(1)若△ACD的面积为16.
①求抛物线解析式;
②S为线段OD上一点,过S作x轴的垂线,交抛物线于点P,将线段SC,SP绕点S顺时针旋转任意相同的角到SC1,SP1的位置,使点C,P的对应点C1,P1都在x轴上方,C1C与P1S交于点M,P1P与x轴交于点N.求![]() 的最大值;
的最大值;
(2)如图2,直线y=x﹣12a与x轴交于点B,点M在抛物线上,且满足∠MAB=75°的点M有且只有两个,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com