
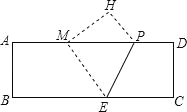
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
【答案】(1)5;(2)![]() ;(3)7+5
;(3)7+5![]() .
.
【解析】
试题分析:(1)由折叠的性质可得PD=PH=3,CD=MH=4,∠H=∠D=90°,利用勾股定理可得答案;(2)先找到使三角形MEF的周长最小的F点,如图1,做点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,由(1)可得AM,利用勾股定理可得ME和NM′,由△AFM′∽△NEM′,利用相似三角形的性质可得AF;(3)由题意可知,ME,QG的长度是个定值,当四边形MEQG的周长最小时,QE与GM的长度和最小,如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,由平行四边形的判定定理可得四边形ERGQ为平行四边形,由平行四边形的性质可得QE=GR,由垂直平分线的性质易得GM=GM′,可得此时MG+EQ最小,于是四边形MEQG的周长最小,在Rt△M′RN中,易得NR,M′R,从而得到四边形MEQG的最小周长值.
试题解析:(1)∵四边形ABCD为矩形,∴CD=AB=4,∠D=90°,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴PD=PH=3,CD=MH=4,∠H=∠D=90°,∴![]() =5;(2)如图1,
=5;(2)如图1,
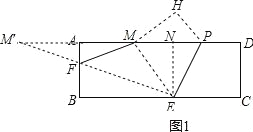 做点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,∴AM=AM′=4,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴∠CEP=∠MEP,∠CEP=∠MPE,∴∠MEP=∠MPE,∴ME=MP=5;在Rt△ENM中,MN=
做点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,∴AM=AM′=4,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴∠CEP=∠MEP,∠CEP=∠MPE,∴∠MEP=∠MPE,∴ME=MP=5;在Rt△ENM中,MN=![]() =
=![]() =3,∴NM′=11,∵AF∥NE,∴△AFM′∽△NEM′,∴
=3,∴NM′=11,∵AF∥NE,∴△AFM′∽△NEM′,∴![]() =
=![]() ,即
,即![]() ,解得:AF=
,解得:AF=![]() ,即AF=
,即AF=![]() 时,△MEF的周长最小;(3)如图2,
时,△MEF的周长最小;(3)如图2,
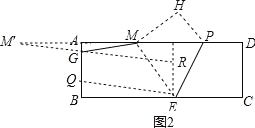 由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,∵ER=GQ,ER∥GQ,∴四边形ERGQ是平行四边形,∴QE=GR,∵GM=GM′,∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,在Rt△M′RN中,NR=4﹣2=2,M′R=
由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,∵ER=GQ,ER∥GQ,∴四边形ERGQ是平行四边形,∴QE=GR,∵GM=GM′,∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,在Rt△M′RN中,NR=4﹣2=2,M′R=![]() =5
=5![]() ,∵ME=5,GQ=2,∴四边形MEQG的最小周长值=5+2+5
,∵ME=5,GQ=2,∴四边形MEQG的最小周长值=5+2+5![]() =7+5
=7+5![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
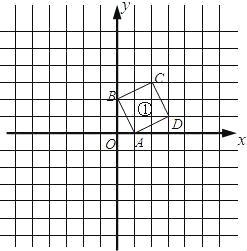
【题目】在平面直角坐标系中,将A(1,0)、B(0,2)、C(2,3)、D(3,1)用线段依次连接起来形成一个图案(图案①).将图案①绕点O逆时针旋转90°得到图案②;以点O为位似中心,位似比为1:2将图案①在位似中心的异侧进行放大得到图案③.
(1)在坐标系中分别画出图案②和图案③;
(2)若点D在图案②中对应的点记为点E,在图案③中对应的点记为点F,则S△DEF= ;
(3)若图案①上任一点P(A、B除外)的坐标为(a,b),图案②中与之对应的点记为点Q,图案③中与之对应的点记为点R,则S△PQR= .(用含有a、b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 正分数、负分数统称分数 B. 零是整数,但不是分数
C. 正整数、负整数统称整数 D. 零既不是正数,也不是负数
查看答案和解析>>
科目:初中数学 来源: 题型:
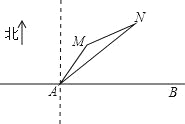
【题目】如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10百米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
(1)求M,N两村之间的距离;
(2)试问村庄N在村庄M的什么方向上?(精确到0.1度)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com