
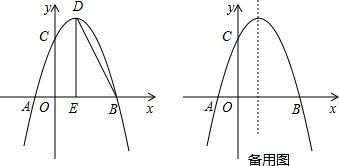
分析 (1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式,再利用配方法将抛物线解析式变形成顶点式即可得出结论;
(2)设线段BF与y轴交点为点F′,设点F′的坐标为(0,m),由相似三角形的判定及性质可得出点F′的坐标,根据点B、F′的坐标利用待定系数法可求出直线BF的解析式,联立直线BF和抛物线的解析式成方程组,解方程组即可求出点F的坐标;
(3)设对角线MN、PQ交于点O′,如图2所示.根据抛物线的对称性结合正方形的性质可得出点P、Q的位置,设出点Q的坐标为(2,2n),由正方形的性质可得出点M的坐标为(2-n,n).由点M在抛物线图象上,即可得出关于n的一元二次方程,解方程可求出n值,代入点Q的坐标即可得出结论.
解答 解:(1)将点B(6,0)、C(0,6)代入y=-$\frac{1}{2}$x2+bx+c中,
得:$\left\{\begin{array}{l}{0=-18+6b+c}\\{6=c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=6}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+2x+6.
∵y=-$\frac{1}{2}$x2+2x+6=-$\frac{1}{2}$(x-2)2+8,
∴点D的坐标为(2,8).
(2)设线段BF与y轴交点为点F′,设点F′的坐标为(0,m),如图1所示.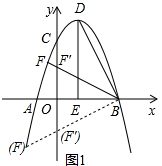
∵∠F′BO=∠FBA=∠BDE,∠F′OB=∠BED=90°,
∴△F′BO∽△BDE,
∴$\frac{OF′}{OB}=\frac{BE}{DE}$.
∵点B(6,0),点D(2,8),
∴点E(2,0),BE=6-2=4,DE=8-0=8,OB=6,
∴OF′=$\frac{BE}{DE}$•OB=3,
∴点F′(0,3)或(0,-3).
设直线BF的解析式为y=kx±3,
则有0=6k+3或0=6k-3,
解得:k=-$\frac{1}{2}$或k=$\frac{1}{2}$,
∴直线BF的解析式为y=-$\frac{1}{2}$x+3或y=$\frac{1}{2}$x-3.
联立直线BF与抛物线的解析式得:$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=-\frac{1}{2}{x}^{2}+2x+6}\end{array}\right.$①或$\left\{\begin{array}{l}{y=\frac{1}{2}x-3}\\{y=-\frac{1}{2}{x}^{2}+2x+6}\end{array}\right.$②,
解方程组①得:$\left\{\begin{array}{l}{x=-1}\\{y=\frac{7}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$(舍去),
∴点F的坐标为(-1,$\frac{7}{2}$);
解方程组②得:$\left\{\begin{array}{l}{x=-3}\\{y=-\frac{9}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$(舍去),
∴点F的坐标为(-3,-$\frac{9}{2}$).
综上可知:点F的坐标为(-1,$\frac{7}{2}$)或(-3,-$\frac{9}{2}$).
(3)设对角线MN、PQ交于点O′,如图2所示.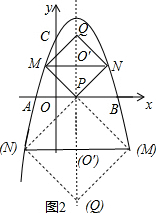
∵点M、N关于抛物线对称轴对称,且四边形MPNQ为正方形,
∴点P为抛物线对称轴与x轴的交点,点Q在抛物线对称轴上,
设点Q的坐标为(2,2n),则点M的坐标为(2-n,n).
∵点M在抛物线y=-$\frac{1}{2}$x2+2x+6的图象上,
∴n=-$\frac{1}{2}(2-n)^{2}$+2(2-n)+6,即n2+2n-16=0,
解得:n1=$\sqrt{17}$-1,n2=-$\sqrt{17}$-1.
∴点Q的坐标为(2,2$\sqrt{17}$-2)或(2,-2$\sqrt{17}$-2).
点评 本题考查了待定系数法求函数解析式、相似三角形的判定及性质、正方形的性质及解一元二次方程,解题的关键是:(1)利用待定系数法求出函数解析式;(2)求出直线BF的解析式;(3)得出关于n的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标利用待定系数法求出函数解析式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
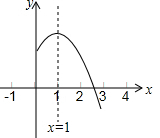 二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).
二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 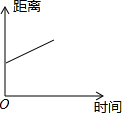 | C. | 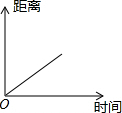 | D. | 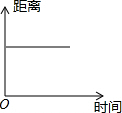 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 绿 化 树 品 种 | A | B | C |
| 每辆货车运载量(株) | 40 | 48 | 32 |
| 每株树苗的价格(元) | 20 | 50 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
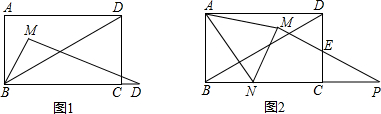
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (3,-1) | C. | (-1,3) | D. | (1,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com