
【题目】如图,⊙O中,![]() =
=![]() ,∠ABC=75°,BC=2,则图中阴影部分的面积是( ).
,∠ABC=75°,BC=2,则图中阴影部分的面积是( ).

A.2+![]() B.2+
B.2+![]() C.4+
C.4+![]() D.
D.![]() +
+![]()
【答案】A
【解析】
根据圆的基本性质可得:AB=AC,从而得出:点A在BC的中垂线上,∠ABC=∠ACB=75°,根据三角形内角和定理,可求出∠BAC,根据圆周角定理可求出∠BOC,从而判定△OBC是等边三角形,同时可证:AD垂直平分BC,从而求出∠BOD,求出AD,然后利用S阴影=S△ABC+S扇形OBC-S△OBC即可求出阴影面积.
解:连接AO并延长交BC于D,连接OB、OC,如下图所示
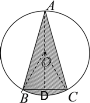
∵![]() =
=![]()
∴AB=AC
∴点A在BC的中垂线上,∠ABC=∠ACB=75°
∴∠BAC=180°-∠ABC-∠ACB=30°
∴∠BOC=60°
∵OB=OC
∴△OBC是等边三角形,点O在BC的中垂线上
∴OB=OC=BC=2,AD垂直平分BC
∴OA=OB=2,OD平分∠BOC
∴∠BOD=![]() ∠BOC=30°
∠BOC=30°
∴OD=OB·cos∠BOD=![]()
∴AD=AO+OD=2+![]()
∴S阴影=S△ABC+S扇形OBC-S△OBC
=![]() AD·BC+
AD·BC+![]() -
-![]() OD·BC
OD·BC
=![]() ×(2+
×(2+![]() )×2+
)×2+![]() -
-![]() ×
×![]() ×2
×2
=2+![]()
故选A.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
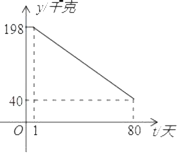
【题目】荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:![]() (1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸是一家水果店的经理.一天,他去水果批发市场,用100元购进甲种水果,用100元购进乙种水果,已知乙种水果比甲种水果多10千克,乙种水果的批发价比甲种水果的批发价低0.5元.
(1)求甲、乙两种水果各购进了多少千克?
(2)如果当天甲、乙两种水果都按2.80元出售,乙种水果很快售完,而甲种水果先售出![]() ,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
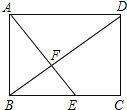
【题目】如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
(1)图中与△ABF相似的三角形(不包括△ABF本身)共有_____个.
(2)若BE=2,AD=5.求:AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
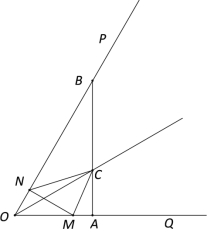
【题目】如图,已知∠POQ=60°,点A、B分别在射线OQ、OP上,且OA=2,OB=4,∠POQ的平分线交AB于C,一动点N从O点出发,以每秒1个单位长度的速度沿射线OP向点B作匀速运动,MN⊥OB交射线OQ于点M.设点N运动的时间为t(0<t<2)秒.
(1)求证:△ONM∽△OAB;
(2)当MN=CM时,求t的值;
(3)设△MNC与△OAB重叠部分的面积为S.请求出S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
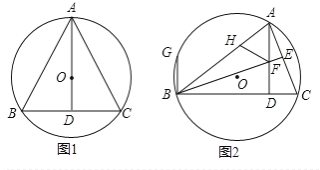
【题目】已知锐角△ABC内接于O,AD⊥BC.垂足为D.
(1)如图1,若![]() ,BD=DC,求∠B的度数.
,BD=DC,求∠B的度数.
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG;
①连接CG,试探究∠ABC,∠ACG的数量关系,并给予证明.
②求证:△AFH是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com