
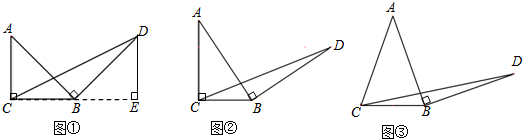
 如图,点E为正方形ABCD的边BC延长线上一点,连接DE.点F为线段DE上一点,连接AF、BF,AF正好平分∠DFB.
如图,点E为正方形ABCD的边BC延长线上一点,连接DE.点F为线段DE上一点,连接AF、BF,AF正好平分∠DFB.分析 (1)作AH⊥BF于H,AG⊥DE于G,由角平分线和正方形的性质得到AG=AH,AB=AD,证得三角形全等,得到∠ABH=∠ADG,因为∠ADG=∠DAF+∠AFD,所以得到结论∠ABF-∠DAF=∠DFA=$\frac{1}{2}$∠DFB;
(2)由锐角三角函数得到tan∠DEB=2,$\frac{DC}{EC}$=$\frac{BF}{EF}$=2,求得EC=$\sqrt{5}$BE=$3\sqrt{5}$,BF=2EF,由勾股定理解得EF=3,BF=6,得到S△EFB=$\frac{1}{2}$BF•EF=$\frac{1}{2}$×6×3=9.
解答  (1)证明:作AH⊥BF于H,AG⊥DE于G,
(1)证明:作AH⊥BF于H,AG⊥DE于G,
∵∠AFG=∠AFB,
∴AG=AH,
∵四边形ABCD是正方形,
∴AB=AD,
在Rt△ABH与Rt△ADG中,$\left\{\begin{array}{l}{AB=AD}\\{AH=AG}\end{array}\right.$,
∴Rt△ABH≌Rt△ADG,
∴∠ABH=∠ADG,
∵∠ADG=∠DAF+∠AFD,
∴∠ABF-∠DAF=∠DFA=$\frac{1}{2}$∠DFB,
(2)解:∵∠ABC=∠ADC=90°,
∴∠ABF+∠FBE=∠GDA+∠CDE=90°,
∴∠EBF=∠CDE,
∴∠DFB=∠DCB=90°,
∵tan∠DEB=2,∴$\frac{DC}{EC}$=$\frac{BF}{EF}$=2,∴EC=$\sqrt{5}$BE=$3\sqrt{5}$,BF=2EF,
∴EF2+(2EF)2=${(3\sqrt{5)}}^{2}$,
EF=3,BF=6,
∴S△EFB=$\frac{1}{2}$BF•EF=$\frac{1}{2}$×6×3=9
点评 本题考查了全等三角形的判定与性质,正方形的性质,勾股定理的应用,三角形的面积公式,辅助线的作法是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M.
如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com