
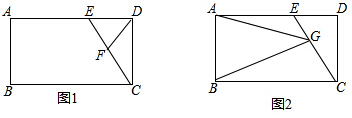
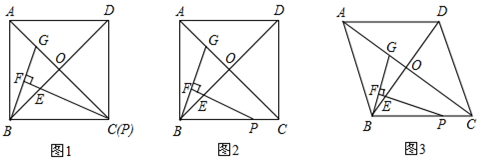
分析 (1)判断出∠ADC=90°,用一个内角是90°平行四边形是矩形;
(2)先利用等角或同角的余角相等判断出∠BAH=∠EAG,∠ABH=∠AEG,从而得到△ABH≌△AEG,即AH=AG,即可;
(3)设出DE=x,利用勾股定理和条件得到 CD=3x,再用三角函数表示出CG=$\frac{2\sqrt{10}}{5}$x,EG=$\frac{3\sqrt{10}}{5}$x,即可得到结论.
解答 (1)∵F为CE的中点,DF=EF,
∴∠ECD=∠FDC,∠CED=∠EDF,
∵∠ECD+∠FDC+∠CED+∠EDF=180°,
∴∠ADC=∠CDF+∠EDF=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD为矩形;
(2)①如图2,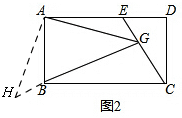
过点A作HA⊥AG,交GB的延长线于点H,
∴∠BAH+∠BAG=90°,
∵∠EAG+∠BAG=90°,
∴∠BAH=∠EAG,
∵BG⊥CE,
∴∠CBG+∠ABG=90°,∠CBG+∠BCG=90°,
∴∠ABG=∠BCG,
∵∠BCG+∠DCE=∠DEC+∠DCE=90°,
∴∠ABG=∠CED,
∴∠ABH=∠AEG,
∵AB=AE,∠BAH=∠EAG
∴△ABH≌△AEG(ASA),
∴AH=AG,
∵∠HAG=90°,
∴∠AGB=45°;
②设DE=x,
∵CD=3DE
∴CD=3DE=3x,
∵∠CDE=90°,
∴CE=$\sqrt{D{E}^{2}+C{D}^{2}}$=$\sqrt{10}$x,
∴sin∠DCE=$\frac{DE}{CE}$=$\frac{x}{\sqrt{10}x}$=$\frac{\sqrt{10}}{10}$,
∵四边形ABCD是矩形,
∴AB=CD=3x,
∴AE=AB=3x,
∴BC=AD=AE+DE=3x+x=4x,
∵BG⊥CE,
∴∠CBG+∠BCE=90°,
∵∠DCE+∠BCE=90°,
∴∠CBG=∠DCE,
∴sin∠CBG=sin∠DCE=$\frac{CG}{BC}$=$\frac{CG}{4x}$=$\frac{\sqrt{10}}{10}$,
∴CG=$\frac{2\sqrt{10}}{5}$x,
∵CE=$\sqrt{10}$x,
∴EG=CE-CG=$\sqrt{10}$x-$\frac{2\sqrt{10}}{5}$x=$\frac{3\sqrt{10}}{5}$x,
∴$\frac{EG}{CG}$=$\frac{\frac{3\sqrt{10}}{5}x}{\frac{2\sqrt{10}}{5}x}$=$\frac{3}{2}$
故答案为$\frac{3}{2}$.
点评 此题是四边形综合题,主要考查了判定直角的方法,勾股定理,锐角三角函数的意义,同角或等角的余角相等,解本题的关键是灵活运用同角或等角的余角相等,判断角相等.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
 我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
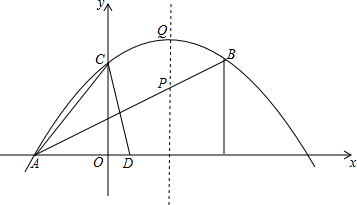 如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.
如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
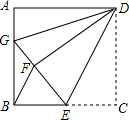 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
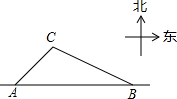 如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)
如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com