解:(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
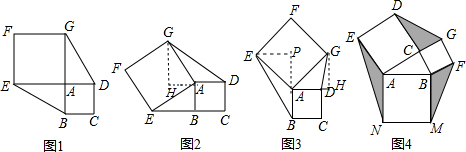
∴AE=AG,AB=AD,∠EAB=∠GAD,
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,如图2,
∴∠AHG=90°,
∵E点旋转到CB的延长线上,
∴∠ABE=90°,∠HAB=90°,
∴∠GAH=∠EAB,
在△AHG和△AEB中
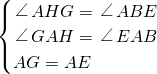
,
∴△AHG≌△AEB,
∴GH=BE,
∵△ABE的面积=

EB•AB,△ADG的面积=

GH•AD,
∴△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,
∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中
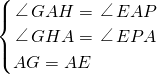
,
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABP的面积=

EP•AB,△ADG的面积=

GH•AD,
∴△ABP的面积=△ADG的面积;
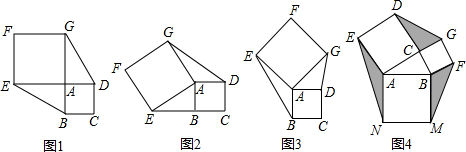
(3)∵AB=5cm,BC=3cm,
∴AC=

=4cm,
∴△ABC的面积=

×3×4=6(cm
2);
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm
2.
故答案为相等;相等;18.
分析:(1)①根据正方形的性质得到AE=AG,AB=AD,∠EAB=∠GAD,根据“SAS”可判断△ABE≌△ADG,则△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,根据等角的余角相等得到∠GAH=∠EAB,根据“AAS”可判断△AHG≌△AEP,则GH=BP,然后根据三角形面积公式得到△ABE的面积=△ADG的面积;
(2)作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,根据等角的余角相等得到∠PAE=∠GAH,根据“AAS”可判断△AHG≌△AEP,所以GH=BP,然后根据三角形面积公式得到△ABP的面积=△ADG的面积;
(3)先根据勾股定理可计算出AC=4cm,则△ABC的面积=

×3×4=6(cm
2);然后根据(2)中的结结论计算阴影部分的面积和的最大值.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了正方形的性质和三角形面积公式.


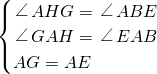 ,
, EB•AB,△ADG的面积=
EB•AB,△ADG的面积= GH•AD,
GH•AD,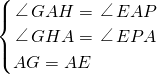 ,
, EP•AB,△ADG的面积=
EP•AB,△ADG的面积= GH•AD,
GH•AD, =4cm,
=4cm, ×3×4=6(cm2);
×3×4=6(cm2); ×3×4=6(cm2);然后根据(2)中的结结论计算阴影部分的面积和的最大值.
×3×4=6(cm2);然后根据(2)中的结结论计算阴影部分的面积和的最大值.

 小学教材完全解读系列答案
小学教材完全解读系列答案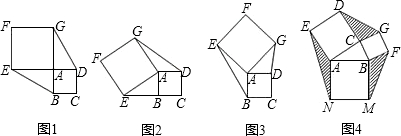
 24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.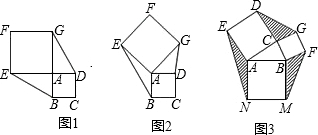
 如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.
如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.